3849. Equal Sum Grid Partition I¶

3849. Equal Sum Grid Partition I

Medium

You are given an m x n matrix grid of positive integers. Your task is to determine if it is possible to make either one horizontal or one vertical cut on the grid such that:

Each of the two resulting sections formed by the cut is non-empty.
The sum of the elements in both sections is equal.

Return true if such a partition exists; otherwise return false.

Example 1:

Input: grid = [[1,4],[2,3]]

Output: true

Explanation:

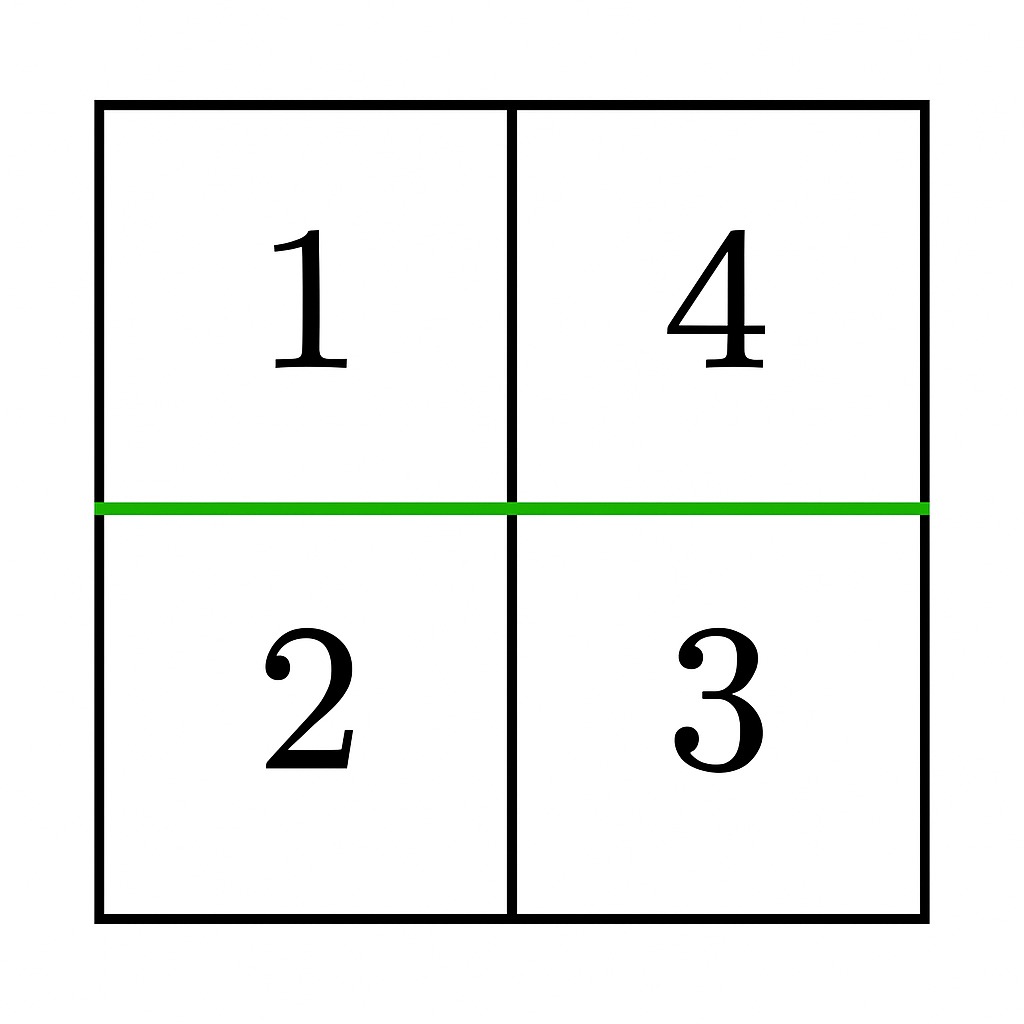
A horizontal cut between row 0 and row 1 results in two non-empty sections, each with a sum of 5. Thus, the answer is true.

Example 2:

Input: grid = [[1,3],[2,4]]

Output: false

Explanation:

No horizontal or vertical cut results in two non-empty sections with equal sums. Thus, the answer is false.

Constraints:

1 <= m == grid.length <= 10⁵
1 <= n == grid[i].length <= 10⁵
2 <= m * n <= 10⁵
1 <= grid[i][j] <= 10⁵

Solution¶

class Solution {
    public boolean canPartitionGrid(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int row_sum[] = new int[n];
        int col_sum[] = new int[m];
        int sum = 0;
        for (int i = 0;  i < n; i++) {
            for (int j = 0; j < m; j++) {
                sum += grid[i][j];
            }
            row_sum[i] = sum;
        }
        sum = 0;
        for (int j = 0; j < m; j++) {
            for (int i = 0; i < n; i++) {
                sum += grid[i][j];
            }
            col_sum[j] = sum;
        }
        for (int i = 0; i < n - 1; i++) {
            int up_sum = row_sum[i];
            int buttom_sum = row_sum[n - 1] - up_sum;
            if (up_sum == buttom_sum) return true;
        }
        for (int j = 0; j < m - 1; j++) {
            int left_sum = col_sum[j];
            int right_sum = col_sum[m - 1] - left_sum;
            if (left_sum == right_sum) return true;
        }    
        return false;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Explanation¶

[Add detailed explanation here]