3809. Properties Graph¶

Difficulty: Medium

3809. Properties Graph

Medium

You are given a 2D integer array properties having dimensions n x m and an integer k.

Define a function intersect(a, b) that returns the number of distinct integers common to both arrays a and b.

Construct an undirected graph where each index i corresponds to properties[i]. There is an edge between node i and node j if and only if intersect(properties[i], properties[j]) >= k, where i and j are in the range [0, n - 1] and i != j.

Return the number of connected components in the resulting graph.

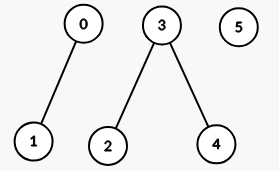
Example 1:

Input: properties = [[1,2],[1,1],[3,4],[4,5],[5,6],[7,7]], k = 1

Output: 3

Explanation:

The graph formed has 3 connected components:

Example 2:

Input: properties = [[1,2,3],[2,3,4],[4,3,5]], k = 2

Output: 1

Explanation:

The graph formed has 1 connected component:

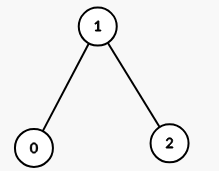
Example 3:

Input: properties = [[1,1],[1,1]], k = 2

Output: 2

Explanation:

intersect(properties[0], properties[1]) = 1, which is less than k. This means there is no edge between properties[0] and properties[1] in the graph.

Constraints:

1 <= n == properties.length <= 100
1 <= m == properties[i].length <= 100
1 <= properties[i][j] <= 100
1 <= k <= m

Solution¶

class Solution {
    static class DSU {
        int parent[], size[];
        public DSU(int n) {
            parent = new int[n + 1];
            size = new int[n + 1];
            for (int i = 0; i <= n; i++) {
                parent[i] = i;
                size[i] = 1;
            }
        }
        public void unite(int u, int v) {
            u = Leader(u); v = Leader(v);
            if (u == v)
                return;
            if (size[v] > size[u]) {
                int temp = u;
                u = v;
                v = temp;
            }
            size[u] += size[v];
            parent[v] = u;
        }
        public int Leader(int u) {
            if (u == parent[u]) 
                return u;
            return parent[u] = Leader(parent[u]);
        }
    }

    public int numberOfComponents(int[][] properties, int k) {
        DSU dsu = new DSU(properties.length + 1);
        for (int i = 0; i < properties.length; i++) {
            HashSet<Integer> curr = new HashSet<>();
            for (int ele : properties[i]) 
                curr.add(ele);
            for (int j = i + 1; j < properties.length; j++) {
                HashSet<Integer> newH = new HashSet<>();
                for (int ele : properties[j]) 
                    newH.add(ele);
                int count = 0;
                for (int ele : curr) 
                    if (newH.contains(ele)) 
                        count++;
                if (count >= k) 
                    dsu.unite(i, j); 
            }
        }        

        int res = 0;
        for (int i = 0; i < properties.length; i++) {
            if (dsu.Leader(i) == i) 
                res++;
        } 
        return res;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here