3748. Sort Matrix By Diagonals¶

Difficulty: Medium

LeetCode Problem View on GitHub

3748. Sort Matrix by Diagonals

Medium

You are given an n x n square matrix of integers grid. Return the matrix such that:

The diagonals in the bottom-left triangle (including the middle diagonal) are sorted in non-increasing order.
The diagonals in the top-right triangle are sorted in non-decreasing order.

Example 1:

Input: grid = [[1,7,3],[9,8,2],[4,5,6]]

Output: [[8,2,3],[9,6,7],[4,5,1]]

Explanation:

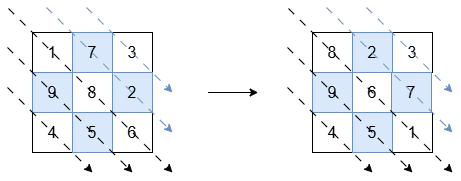
The diagonals with a black arrow (bottom-left triangle) should be sorted in non-increasing order:

[1, 8, 6] becomes [8, 6, 1].
[9, 5] and [4] remain unchanged.

The diagonals with a blue arrow (top-right triangle) should be sorted in non-decreasing order:

[7, 2] becomes [2, 7].
[3] remains unchanged.

Example 2:

Input: grid = [[0,1],[1,2]]

Output: [[2,1],[1,0]]

Explanation:

The diagonals with a black arrow must be non-increasing, so [0, 2] is changed to [2, 0]. The other diagonals are already in the correct order.

Example 3:

Input: grid = [[1]]

Output: [[1]]

Explanation:

Diagonals with exactly one element are already in order, so no changes are needed.

Constraints:

grid.length == grid[i].length == n
1 <= n <= 10
-10⁵ <= grid[i][j] <= 10⁵

Solution¶

class Solution {
    public int[][] sortMatrix(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int cr = n - 1, cc = 0;
        while (cr >= 0) {
            int i = cr, j = 0;
            ArrayList<Integer> temp = new ArrayList<>();
            while (i < n && j < m) temp.add(grid[i++][j++]);
            Collections.sort(temp); Collections.reverse(temp);
            i = cr; j = 0;
            int idx = 0;
            while (i < n && j < m) grid[i++][j++] = temp.get(idx++); 
            cr--;
        }
        cr = 0; cc = m - 1;
        while (cc >= 1) {
            int i = cr, j = cc;
            ArrayList<Integer> temp = new ArrayList<>();
            while (i < n && j < m) temp.add(grid[i++][j++]);
            Collections.sort(temp);
            i = 0; j = cc;
            int idx = 0;
            while (i < n && j < m) grid[i++][j++] = temp.get(idx++);
            cc--;
        }
        return grid;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here