3743. Reschedule Meetings For Maximum Free Time I¶

Difficulty: Medium

3743. Reschedule Meetings for Maximum Free Time I

Medium

You are given an integer eventTime denoting the duration of an event, where the event occurs from time t = 0 to time t = eventTime.

You are also given two integer arrays startTime and endTime, each of length n. These represent the start and end time of n non-overlapping meetings, where the i^th meeting occurs during the time [startTime[i], endTime[i]].

You can reschedule at most k meetings by moving their start time while maintaining the same duration, to maximize the longest continuous period of free time during the event.

The relative order of all the meetings should stay the same and they should remain non-overlapping.

Return the maximum amount of free time possible after rearranging the meetings.

Note that the meetings can not be rescheduled to a time outside the event.

Example 1:

Input: eventTime = 5, k = 1, startTime = [1,3], endTime = [2,5]

Output: 2

Explanation:

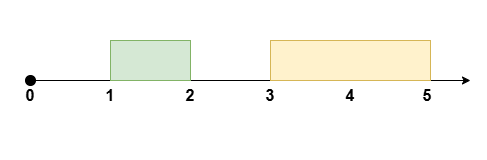
Reschedule the meeting at [1, 2] to [2, 3], leaving no meetings during the time [0, 2].

Example 2:

Input: eventTime = 10, k = 1, startTime = [0,2,9], endTime = [1,4,10]

Output: 6

Explanation:

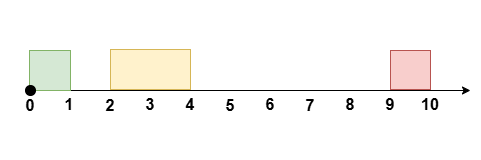
Reschedule the meeting at [2, 4] to [1, 3], leaving no meetings during the time [3, 9].

Example 3:

Input: eventTime = 5, k = 2, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]

Output: 0

Explanation:

There is no time during the event not occupied by meetings.

Constraints:

1 <= eventTime <= 10⁹
n == startTime.length == endTime.length
2 <= n <= 10⁵
1 <= k <= n
0 <= startTime[i] < endTime[i] <= eventTime
endTime[i] <= startTime[i + 1] where i lies in the range [0, n - 2].

Solution¶

class Solution {
    public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {
        int low = 0, high = (int)(1e9);
        int ans = -1;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (check(eventTime, k, startTime, endTime, mid)) {
                ans = mid;
                low = mid + 1;
            }
            else 
                high = mid - 1;
        }
        return Math.max(ans, 0);
    }

    private boolean check(int eventTime, int k, int startTime[], int endTime[], int mid) {
        ArrayList<Integer> res = new ArrayList<>();
        res.add(startTime[0]);
        for (int i = 1; i < startTime.length; i++) 
            res.add(startTime[i] - endTime[i - 1]);
        res.add(eventTime - endTime[startTime.length - 1]);
        int sum = 0;
        for (int i = 0; i < k + 1; i++) {
            sum += res.get(i);
        }
        int maxi = sum;
        for (int i = k + 1; i < res.size(); i++) {
            sum += res.get(i) - res.get(i - (k + 1));
            maxi = Math.max(maxi, sum);
        }
        return maxi >= mid;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here