3733. Length Of Longest V Shaped Diagonal Segment¶

Difficulty: Hard

LeetCode Problem View on GitHub

3733. Length of Longest V-Shaped Diagonal Segment

Hard

You are given a 2D integer matrix grid of size n x m, where each element is either 0, 1, or 2.

A V-shaped diagonal segment is defined as:

The segment starts with 1.
The subsequent elements follow this infinite sequence: 2, 0, 2, 0, ....
The segment:
- Starts along a diagonal direction (top-left to bottom-right, bottom-right to top-left, top-right to bottom-left, or bottom-left to top-right).
- Continues the sequence in the same diagonal direction.
- Makes at most one clockwise 90-degree turn to another diagonal direction while maintaining the sequence.

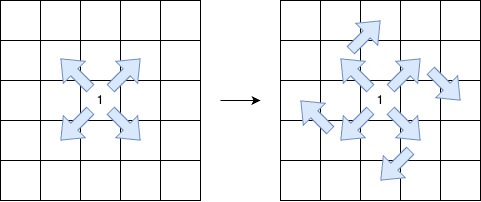
Return the length of the longest V-shaped diagonal segment. If no valid segment exists, return 0.

Example 1:

Input: grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 5

Explanation:

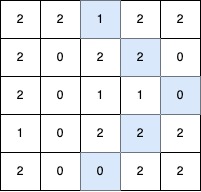
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,2) → (1,3) → (2,4), takes a 90-degree clockwise turn at (2,4), and continues as (3,3) → (4,2).

Example 2:

Input: grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

Output: 4

Explanation:

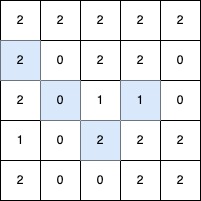
The longest V-shaped diagonal segment has a length of 4 and follows these coordinates: (2,3) → (3,2), takes a 90-degree clockwise turn at (3,2), and continues as (2,1) → (1,0).

Example 3:

Input: grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

Output: 5

Explanation:

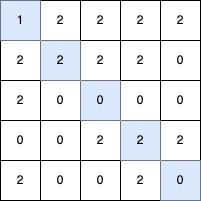
The longest V-shaped diagonal segment has a length of 5 and follows these coordinates: (0,0) → (1,1) → (2,2) → (3,3) → (4,4).

Example 4:

Input: grid = [[1]]

Output: 1

Explanation:

The longest V-shaped diagonal segment has a length of 1 and follows these coordinates: (0,0).

Constraints:

n == grid.length
m == grid[i].length
1 <= n, m <= 500
grid[i][j] is either 0, 1 or 2.

Solution¶

class Solution {
    int dir[][] = {{1, 1}, {1, -1}, {-1, -1}, {-1, 1}};
    private int dp[][][][];
    public int lenOfVDiagonal(int[][] grid) {
        int n = grid.length, m = grid[0].length; 
        int maxi = 0;

        dp = new int[n + 1][m + 1][dir.length + 1][2];
        for (int current[][][] : dp) {
            for (int current1[][] : current) {
                for (int current2[] : current1) 
                    Arrays.fill(current2, -1);
            }
        } 

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 1) {
                    for (int k = 0; k < 4; k++) {
                        maxi = Math.max(maxi, solve(i, j, k, 1, grid));
                    }
                }
            }
        }

        return maxi;
    }

    private int solve(int currRow, int currCol, int currDirIdx, int canRotate, int grid[][]) {
        if (currRow < 0 || currCol < 0 || currRow >= grid.length || currCol >= grid[0].length)
            return 0;

        if (dp[currRow][currCol][currDirIdx][canRotate] != -1)
            return dp[currRow][currCol][currDirIdx][canRotate];

        if (grid[currRow][currCol] == 1) {
            int nextRow = currRow + dir[currDirIdx][0], nextCol = currCol + dir[currDirIdx][1];
            int op1 = 1, op2 = 0;
            if (nextRow < grid.length && nextCol < grid[0].length && nextRow >= 0 && nextCol >= 0)
                if (grid[nextRow][nextCol] == 2)
                    op1 += 1 + solve(nextRow, nextCol, currDirIdx, canRotate, grid);

            return dp[currRow][currCol][currDirIdx][canRotate] = op1;
        }

        else if (grid[currRow][currCol] == 2) {
            int nextRow = currRow + dir[currDirIdx][0], nextCol = currCol + dir[currDirIdx][1];
            int op1 = 0, op2 = 0;
            if (nextRow < grid.length && nextCol < grid[0].length && nextRow >= 0 && nextCol >= 0) {
                if (grid[nextRow][nextCol] == 0) 
                    op1 = 1 + solve(nextRow, nextCol, currDirIdx, canRotate, grid);      
            }
            //or rotate it from here;
            if (canRotate == 1) {
                int nextDirIdx = (currDirIdx + 1) % 4;
                int newNextRow = currRow + dir[nextDirIdx][0], newNextCol = currCol + dir[nextDirIdx][1];
                if (newNextRow >= 0 && newNextRow < grid.length && newNextCol >= 0 && newNextCol < grid[0].length) {
                    if (grid[newNextRow][newNextCol] == 0) {
                        op2 = 1 + solve(newNextRow, newNextCol, nextDirIdx, 0, grid);
                    }
                }
            }
            return dp[currRow][currCol][currDirIdx][canRotate] = Math.max(op1, op2);
        }

        else if (grid[currRow][currCol] == 0) {
            int nextRow = currRow + dir[currDirIdx][0], nextCol = currCol + dir[currDirIdx][1];
            int op1 = 0, op2 = 0;
            if (nextRow < grid.length && nextCol < grid[0].length && nextRow >= 0 && nextCol >= 0) {
                if (grid[nextRow][nextCol] == 2)
                    op1 = 1 + solve(nextRow, nextCol, currDirIdx, canRotate, grid);      
            }
            //or rotate it from here;
            if (canRotate == 1) {
                int nextDirIdx = (currDirIdx + 1) % 4;
                int newNextRow = currRow + dir[nextDirIdx][0], newNextCol = currCol + dir[nextDirIdx][1];
                if (newNextRow >= 0 && newNextRow < grid.length && newNextCol >= 0 && newNextCol < grid[0].length) {
                    if (grid[newNextRow][newNextCol] == 2) {
                        op2 = 1 + solve(newNextRow, newNextCol, nextDirIdx, 0, grid);
                    }
                }
            }  
            return dp[currRow][currCol][currDirIdx][canRotate] = Math.max(op1, op2); 
        }
        return 0;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here