3645. Maximize The Number Of Target Nodes After Connecting Trees Ii¶

Difficulty: Hard

3645. Maximize the Number of Target Nodes After Connecting Trees II

Hard

There exist two undirected trees with n and m nodes, labeled from [0, n - 1] and [0, m - 1], respectively.

You are given two 2D integer arrays edges1 and edges2 of lengths n - 1 and m - 1, respectively, where edges1[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the first tree and edges2[i] = [u_i, v_i] indicates that there is an edge between nodes u_i and v_i in the second tree.

Node u is target to node v if the number of edges on the path from u to v is even. Note that a node is always target to itself.

Return an array of n integers answer, where answer[i] is the maximum possible number of nodes that are target to node i of the first tree if you had to connect one node from the first tree to another node in the second tree.

Note that queries are independent from each other. That is, for every query you will remove the added edge before proceeding to the next query.

Example 1:

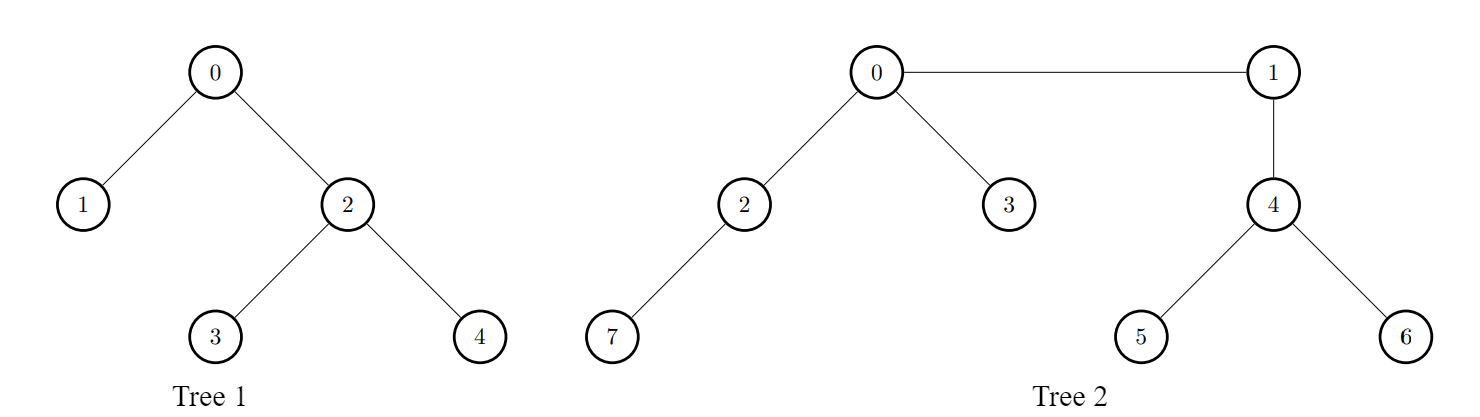
Input: edges1 = [[0,1],[0,2],[2,3],[2,4]], edges2 = [[0,1],[0,2],[0,3],[2,7],[1,4],[4,5],[4,6]]

Output: [8,7,7,8,8]

Explanation:

For i = 0, connect node 0 from the first tree to node 0 from the second tree.
For i = 1, connect node 1 from the first tree to node 4 from the second tree.
For i = 2, connect node 2 from the first tree to node 7 from the second tree.
For i = 3, connect node 3 from the first tree to node 0 from the second tree.
For i = 4, connect node 4 from the first tree to node 4 from the second tree.

Example 2:

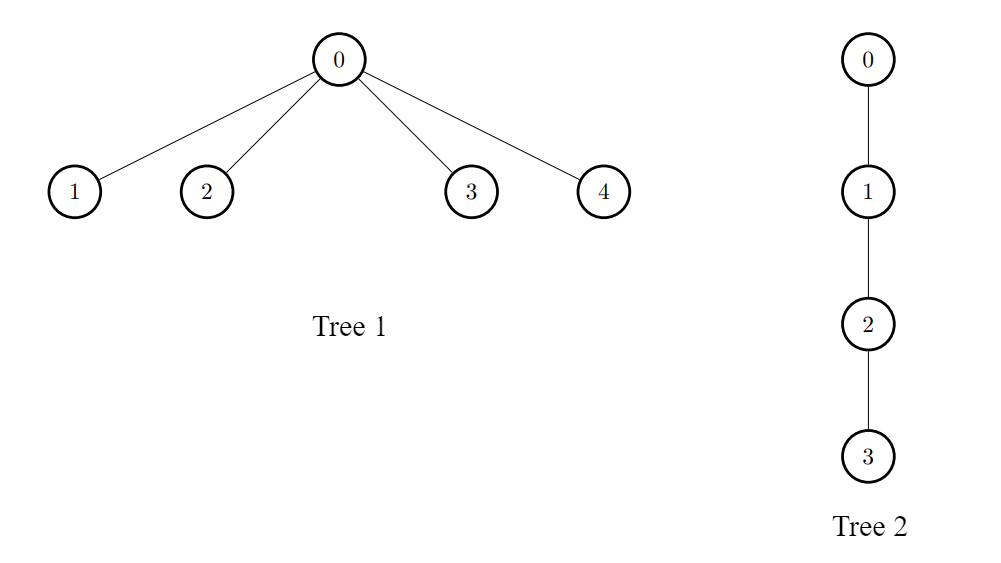
Input: edges1 = [[0,1],[0,2],[0,3],[0,4]], edges2 = [[0,1],[1,2],[2,3]]

Output: [3,6,6,6,6]

Explanation:

For every i, connect node i of the first tree with any node of the second tree.

Constraints:

2 <= n, m <= 10⁵
edges1.length == n - 1
edges2.length == m - 1
edges1[i].length == edges2[i].length == 2
edges1[i] = [a_i, b_i]
0 <= a_i, b_i < n
edges2[i] = [u_i, v_i]
0 <= u_i, v_i < m
The input is generated such that edges1 and edges2 represent valid trees.

Solution¶

import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Queue;

class Solution {
    public int[] maxTargetNodes(int[][] edges1, int[][] edges2) {
        int n = edges1.length + 1, m = edges2.length + 1;
        List<Integer>[] g1 = new ArrayList[n], g2 = new ArrayList[m];
        for (int i = 0; i < n; ++i)
            g1[i] = new ArrayList<>();
        for (int i = 0; i < m; ++i)
            g2[i] = new ArrayList<>();
        for (int[] e : edges1) {
            g1[e[0]].add(e[1]);
            g1[e[1]].add(e[0]);
        }
        for (int[] e : edges2) {
            g2[e[0]].add(e[1]);
            g2[e[1]].add(e[0]);
        }

        int[] depth1 = new int[n], count1 = new int[2];
        bfsDepthParity(g1, depth1, count1);
        int[] depth2 = new int[m], count2 = new int[2];
        bfsDepthParity(g2, depth2, count2);

        int[] ans = new int[n];
        int max2 = Math.max(count2[0], count2[1]);
        for (int i = 0; i < n; ++i) {
            int parity = depth1[i] % 2;
            ans[i] = count1[parity] + max2;
        }
        return ans;
    }

    private void bfsDepthParity(List<Integer>[] g, int[] depth, int[] count) {
        Arrays.fill(depth, -1);
        Queue<Integer> q = new ArrayDeque<>();
        q.add(0);
        depth[0] = 0;
        while (!q.isEmpty()) {
            int u = q.poll();
            count[depth[u] % 2]++;
            for (int v : g[u]) {
                if (depth[v] == -1) {
                    depth[v] = depth[u] + 1;
                    q.add(v);
                }
            }
        }
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here