3459. Find The Minimum Area To Cover All Ones Ii¶

Difficulty: Hard

3459. Find the Minimum Area to Cover All Ones II

Hard

You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1's in grid lie inside these rectangles.

Return the minimum possible sum of the area of these rectangles.

Note that the rectangles are allowed to touch.

Example 1:

Input: grid = [[1,0,1],[1,1,1]]

Output: 5

Explanation:

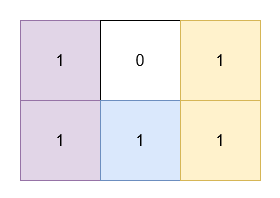
The 1's at (0, 0) and (1, 0) are covered by a rectangle of area 2.
The 1's at (0, 2) and (1, 2) are covered by a rectangle of area 2.
The 1 at (1, 1) is covered by a rectangle of area 1.

Example 2:

Input: grid = [[1,0,1,0],[0,1,0,1]]

Output: 5

Explanation:

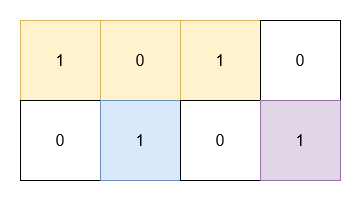
The 1's at (0, 0) and (0, 2) are covered by a rectangle of area 3.
The 1 at (1, 1) is covered by a rectangle of area 1.
The 1 at (1, 3) is covered by a rectangle of area 1.

Constraints:

1 <= grid.length, grid[i].length <= 30
grid[i][j] is either 0 or 1.
The input is generated such that there are at least three 1's in grid.

Solution¶

class Solution {
    public int minimumSum(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        int res = Integer.MAX_VALUE;
        res = Math.min(res, getAns(grid));

        grid = rightRotate(grid);

        res = Math.min(res, getAns(grid));
        return res;
    }

    private int getAns(int grid[][]) {
        int n = grid.length, m = grid[0].length;
        int res = Integer.MAX_VALUE;
        for (int i = 0; i <= n - 2; i++) {
            for (int j = 0; j <= m - 2; j++) {
                int r1 = minSum1(0, i, 0, m - 1, grid);
                int r2 = minSum1(i + 1, n - 1, 0, j, grid);
                int r3 = minSum1(i + 1, n - 1, j + 1, m - 1, grid);
                res = Math.min(res, r1 + r2 + r3);
            }
        }

        for (int i = 0; i <= n - 2; i++) {
            for (int j = 0; j <= m - 2; j++) {
                int r1 = minSum1(0, i, 0, j, grid);
                int r2 = minSum1(0, i, j + 1, m - 1, grid);
                int r3 = minSum1(i + 1, n - 1, 0, m - 1, grid);
                res = Math.min(res, r1 + r2 + r3);
            }
        }

        for (int i1 = 0; i1 <= n - 3; i1++) {
            for (int i2 = i1 + 1; i2 <= n - 2; i2++) {
                int r1 = minSum1(0, i1, 0, m - 1, grid);
                int r2 = minSum1(i1 + 1, i2, 0, m - 1, grid);
                int r3 = minSum1(i2 + 1, n - 1, 0, m - 1, grid);
                res = Math.min(res, r1 + r2 + r3);
            }
        }
        return res;
    }

    private int[][] rightRotate(int grid[][]) {
        int n = grid.length, m = grid[0].length;
        int[][] res = new int[m][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++)
                res[j][n - 1 - i] = grid[i][j];
        }
        grid = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++)
                grid[i][j] = res[i][j];
        }
        return grid;
    }

    private int minSum1(int startRow, int endRow, int startCol, int endCol, int grid[][]) {
        int n = grid.length, m = grid[0].length;
        int minX = Integer.MAX_VALUE, minY = Integer.MAX_VALUE;
        int maxX = Integer.MIN_VALUE, maxY = Integer.MIN_VALUE;
        for (int i = startRow; i <= endRow; i++) {
            for (int j = startCol; j <= endCol; j++) {
                if (grid[i][j] == 1) {
                    minX = Math.min(minX, i);
                    maxX = Math.max(maxX, i);
                    minY = Math.min(minY, j);
                    maxY = Math.max(maxY, j);
                }
            }
        }
        if (maxX == Integer.MIN_VALUE)
            return 0;
        return (maxX - minX + 1) * (maxY - minY + 1);
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here