3278. Find The Number Of Ways To Place People I¶

Input: points = [[1,1],[2,2],[3,3]]

Output: 0

Explanation:

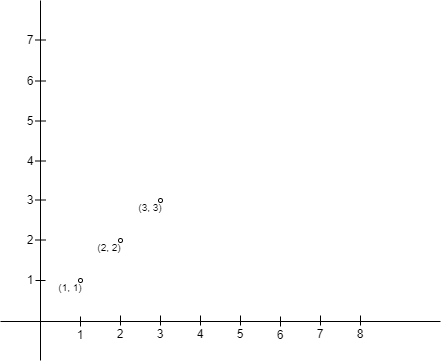
There is no way to choose A and B so A is on the upper left side of B.

Input: points = [[6,2],[4,4],[2,6]]

Output: 2

Explanation:

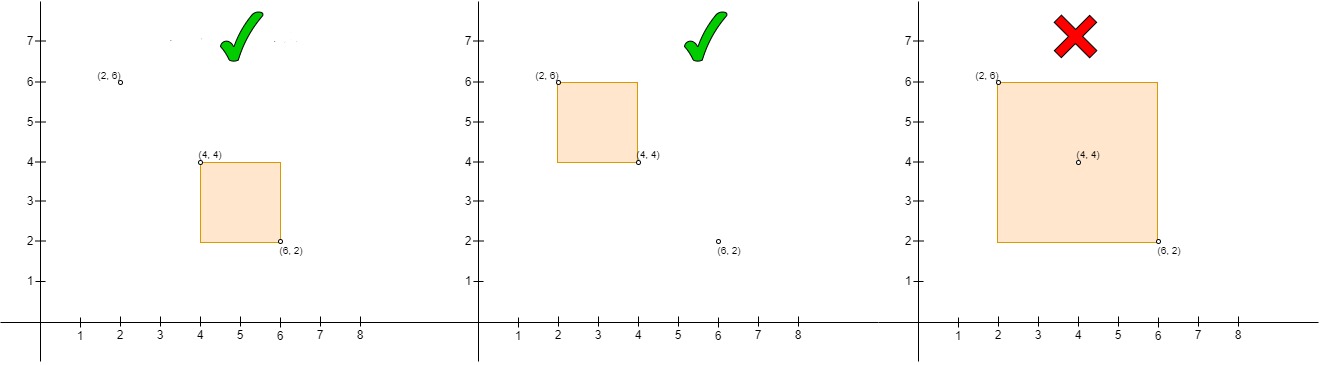
• The left one is the pair (points[1], points[0]), where points[1] is on the upper left side of points[0] and the rectangle is empty.
• The middle one is the pair (points[2], points[1]), same as the left one it is a valid pair.
• The right one is the pair (points[2], points[0]), where points[2] is on the upper left side of points[0], but points[1] is inside the rectangle so it's not a valid pair.

Input: points = [[3,1],[1,3],[1,1]]

Output: 2

Explanation:

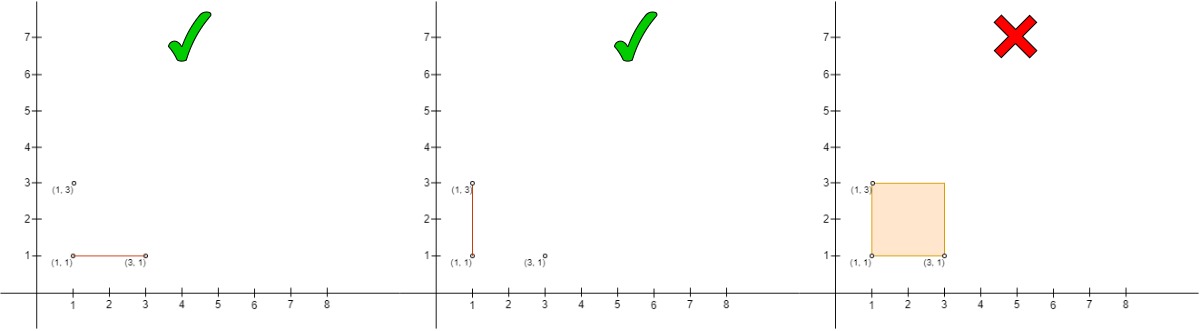
• The left one is the pair (points[2], points[0]), where points[2] is on the upper left side of points[0] and there are no other points on the line they form. Note that it is a valid state when the two points form a line.
• The middle one is the pair (points[1], points[2]), it is a valid pair same as the left one.
• The right one is the pair (points[1], points[0]), it is not a valid pair as points[2] is on the border of the rectangle.

class Solution {
    public int numberOfPairs(int[][] points) {
        int n = points.length;
        int count = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i == j) continue;
                if (valid(i, j, points)) 
                    count++; 
            }
        }    
        return count;
    }
    private boolean valid(int s, int e, int arr[][]) {
        int n = arr.length;
        if (arr[s][0] > arr[e][0] || arr[s][1] < arr[e][1]) 
            return false;
        for (int i = 0; i < n; i++) {
            if (i == s || i == e) 
                continue;
            if (arr[i][0] >= arr[s][0] && arr[i][0] <= arr[e][0] && arr[i][1] <= arr[s][1] && arr[i][1] >= arr[e][1]) {
                return false;
            } 
        }
        return true;
    }
}