3217. Number Of Possible Sets Of Closing Branches¶
Difficulty: Hard
LeetCode Problem View on GitHub
3217. Number of Possible Sets of Closing Branches
Hard
There is a company with n branches across the country, some of which are connected by roads. Initially, all branches are reachable from each other by traveling some roads.
The company has realized that they are spending an excessive amount of time traveling between their branches. As a result, they have decided to close down some of these branches (possibly none). However, they want to ensure that the remaining branches have a distance of at most maxDistance from each other.
The distance between two branches is the minimum total traveled length needed to reach one branch from another.
You are given integers n, maxDistance, and a 0-indexed 2D array roads, where roads[i] = [ui, vi, wi] represents the undirected road between branches ui and vi with length wi.
Return the number of possible sets of closing branches, so that any branch has a distance of at most maxDistance from any other.
Note that, after closing a branch, the company will no longer have access to any roads connected to it.
Note that, multiple roads are allowed.
Example 1:
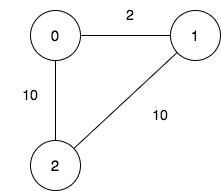
Input: n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]] Output: 5 Explanation: The possible sets of closing branches are: - The set [2], after closing, active branches are [0,1] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 5 possible sets of closing branches.
Example 2:
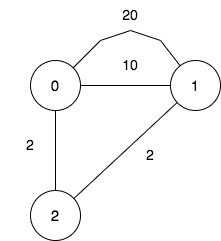
Input: n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]] Output: 7 Explanation: The possible sets of closing branches are: - The set [], after closing, active branches are [0,1,2] and they are reachable to each other within distance 4. - The set [0], after closing, active branches are [1,2] and they are reachable to each other within distance 2. - The set [1], after closing, active branches are [0,2] and they are reachable to each other within distance 2. - The set [0,1], after closing, the active branch is [2]. - The set [1,2], after closing, the active branch is [0]. - The set [0,2], after closing, the active branch is [1]. - The set [0,1,2], after closing, there are no active branches. It can be proven, that there are only 7 possible sets of closing branches.
Example 3:
Input: n = 1, maxDistance = 10, roads = [] Output: 2 Explanation: The possible sets of closing branches are: - The set [], after closing, the active branch is [0]. - The set [0], after closing, there are no active branches. It can be proven, that there are only 2 possible sets of closing branches.
Constraints:
1 <= n <= 101 <= maxDistance <= 1050 <= roads.length <= 1000roads[i].length == 30 <= ui, vi <= n - 1ui != vi1 <= wi <= 1000- All branches are reachable from each other by traveling some roads.
Solution¶
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.HashSet;
import java.util.Objects;
import java.util.PriorityQueue;
class Solution {
private ArrayList<ArrayList<Integer >> sequences;
private int count;
private ArrayList<ArrayList<Pair >> adj;
static class Pair {
int node, weight;
public Pair(int node, int weight) {
this.node = node;
this.weight = weight;
}
@Override
public String toString() {
return "(" + node + ", " + weight + ")";
}
@Override
public boolean equals(Object obj) {
if (this == obj)
return true;
if (obj == null || getClass() != obj.getClass())
return false;
Pair current = (Pair)(obj);
return current.node == node && current.weight == weight;
}
@Override
public int hashCode() {
return Objects.hash(node, weight);
}
}
static class custom_sort implements Comparator<Pair> {
@Override
public int compare(Pair first, Pair second) {
int op1 = Integer.compare(first.weight, second.weight);
if (op1 != 0)
return op1;
return Integer.compare(first.node, second.node);
}
}
static class road_custom_sort implements Comparator<int[]> {
@Override
public int compare(int first[], int second[]) {
int op1 = Integer.compare(first[2], second[2]);
if (op1 != 0)
return op1;
int op2 = Integer.compare(first[1], second[1]);
if (op2 != 0)
return op2;
return Integer.compare(first[0], second[0]);
}
}
public int numberOfSets(int n, int maxDistance, int[][] roads) {
int arr[] = new int[n];
for (int i = 0; i < n; i++)
arr[i] = i;
sequences = new ArrayList<>();
count = 0;
getSequences(0, new ArrayList<>(), arr);
Arrays.sort(roads, new road_custom_sort());
for (ArrayList<Integer> seq : sequences) {
if (check(seq, roads, maxDistance, n) == true)
count++;
}
return count;
}
private boolean check(ArrayList<Integer> seq, int[][] roads, int maxDistance, int n) {
adj = new ArrayList<>();
HashSet<Integer> set = new HashSet<>();
for (int ele : seq)
set.add(ele);
for (int i = 0; i <= n + 1; i++)
adj.add(new ArrayList<>());
HashSet<Pair> occurredEdges = new HashSet<>();
for (int edge[] : roads) {
int u = edge[0], v = edge[1], w = edge[2];
if (occurredEdges.contains(new Pair(u, v)))
continue;
if (!set.contains(u) && !set.contains(v)) {
adj.get(u).add(new Pair(v, w));
adj.get(v).add(new Pair(u, w));
occurredEdges.add(new Pair(u, v));
occurredEdges.add(new Pair(v, u));
}
}
/*set --> i don't want these nodes */
int dist[] = new int[n + 1];
Arrays.fill(dist, Integer.MAX_VALUE / 10);
if (set.size() == n)
return true;
int start_node = -1;
for (int i = 0; i < n; i++) {
if (!set.contains(i)) {
start_node = i;
break;
}
}
HashSet<Integer> dfsGot = new HashSet<>();
int vis[] = new int[n + 1];
dfsReachCheck(start_node, -1, dfsGot, vis);
for (int i = 0; i < n; i++) {
if (!set.contains(i)) {
if (!dfsGot.contains(i))
return false;
}
}
return dfsDistCheck(start_node, adj, set, maxDistance, n, seq);
}
private boolean dfsDistCheck(int start_node, ArrayList<ArrayList<Pair >> adj, HashSet<Integer> set, int maxDistance, int n, ArrayList<Integer> seq) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j)
continue;
if (set.contains(i) || set.contains(j))
continue;
if (computeDistance(i, j, n, adj) > maxDistance)
return false;
}
}
return true;
}
private int computeDistance(int u, int v, int n, ArrayList<ArrayList<Pair >> adj) {
PriorityQueue<Pair> pq = new PriorityQueue<>(new custom_sort());
pq.offer(new Pair(u, 0));
int dist[] = new int[n + 1];
Arrays.fill(dist, Integer.MAX_VALUE / 10);
dist[u] = 0;
while (pq.size() > 0) {
int curr_node = pq.peek().node;
int curr_dist = pq.peek().weight;
pq.poll();
for (int i = 0; i < adj.get(curr_node).size(); i++) {
int child_node = adj.get(curr_node).get(i).node;
int child_dist = adj.get(curr_node).get(i).weight;
if (dist[child_node] > curr_dist + child_dist) {
dist[child_node] = curr_dist + child_dist;
pq.offer(new Pair(child_node, dist[child_node]));
}
}
}
return dist[v];
}
private void dfsReachCheck(int u, int par, HashSet<Integer> dfsGot, int vis[]) {
dfsGot.add(u);
vis[u] = 1;
for (Pair x : adj.get(u)) {
if (vis[x.node] == 0)
dfsReachCheck(x.node, u, dfsGot, vis);
}
}
private void getSequences(int ind, ArrayList<Integer> current, int arr[]) {
if (ind == arr.length) {
sequences.add(new ArrayList<>(current));
return;
}
current.add(arr[ind]);
getSequences(ind + 1, current, arr);
current.remove(current.size() - 1);
getSequences(ind + 1, current, arr);
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here