3191. Maximum Score After Applying Operations On A Tree¶

Difficulty: Medium

3191. Maximum Score After Applying Operations on a Tree

Medium

There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length n - 1, where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

You are also given a 0-indexed integer array values of length n, where values[i] is the value associated with the i^th node.

You start with a score of 0. In one operation, you can:

Pick any node i.
Add values[i] to your score.
Set values[i] to 0.

A tree is healthy if the sum of values on the path from the root to any leaf node is different than zero.

Return the maximum score you can obtain after performing these operations on the tree any number of times so that it remains healthy.

Example 1:

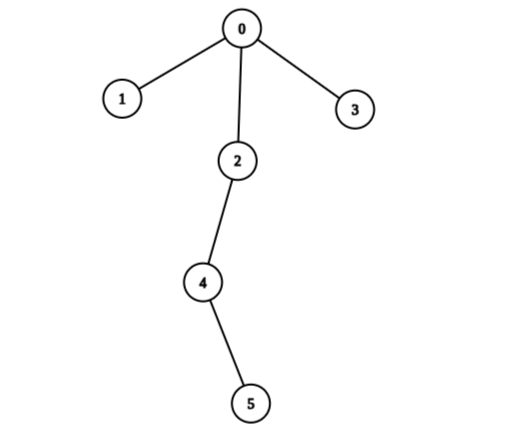
Input: edges = [[0,1],[0,2],[0,3],[2,4],[4,5]], values = [5,2,5,2,1,1]
Output: 11
Explanation: We can choose nodes 1, 2, 3, 4, and 5. The value of the root is non-zero. Hence, the sum of values on the path from the root to any leaf is different than zero. Therefore, the tree is healthy and the score is values[1] + values[2] + values[3] + values[4] + values[5] = 11.
It can be shown that 11 is the maximum score obtainable after any number of operations on the tree.

Example 2:

Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [20,10,9,7,4,3,5]
Output: 40
Explanation: We can choose nodes 0, 2, 3, and 4.
- The sum of values on the path from 0 to 4 is equal to 10.
- The sum of values on the path from 0 to 3 is equal to 10.
- The sum of values on the path from 0 to 5 is equal to 3.
- The sum of values on the path from 0 to 6 is equal to 5.
Therefore, the tree is healthy and the score is values[0] + values[2] + values[3] + values[4] = 40.
It can be shown that 40 is the maximum score obtainable after any number of operations on the tree.

Constraints:

2 <= n <= 2 * 10⁴
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
values.length == n
1 <= values[i] <= 10⁹
The input is generated such that edges represents a valid tree.

Solution¶

class Solution {
    private ArrayList<ArrayList<Integer>> adj;
    private int dp[][];
    private int cost[];
    public long maximumScoreAfterOperations(int[][] edges, int[] values) {
        int n = values.length;
        adj = new ArrayList<>();
        for (int i = 0; i <= n + 1; i++)
            adj.add(new ArrayList<>());
        for (int edge[] : edges) {
            int u = edge[0], v = edge[1];
            adj.get(u).add(v);
            adj.get(v).add(u);
        }
        cost = new int[n];
        for (int i = 0; i < n; i++) 
            cost[i] = values[i];
        long total = 0;
        for (int ele : cost) 
            total += ele;
        return total - dfs(0, -1);
    }
    private long dfs(int u, int par) {
        if (adj.get(u).size() == 1 && u != 0) {
            return cost[u] * 1L;
        }

        long current = 0;
        for (int v : adj.get(u)) {
            if (v != par) {
                current += dfs(v, u);
            }
        }
        return Math.min(current, cost[u]);
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here