2914. Find The Safest Path In A Grid¶

Difficulty: Medium

2914. Find the Safest Path in a Grid

Medium

You are given a 0-indexed 2D matrix grid of size n x n, where (r, c) represents:

A cell containing a thief if grid[r][c] = 1
An empty cell if grid[r][c] = 0

You are initially positioned at cell (0, 0). In one move, you can move to any adjacent cell in the grid, including cells containing thieves.

The safeness factor of a path on the grid is defined as the minimum manhattan distance from any cell in the path to any thief in the grid.

Return the maximum safeness factor of all paths leading to cell (n - 1, n - 1).

An adjacent cell of cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) and (r - 1, c) if it exists.

The Manhattan distance between two cells (a, b) and (x, y) is equal to |a - x| + |b - y|, where |val| denotes the absolute value of val.

Example 1:

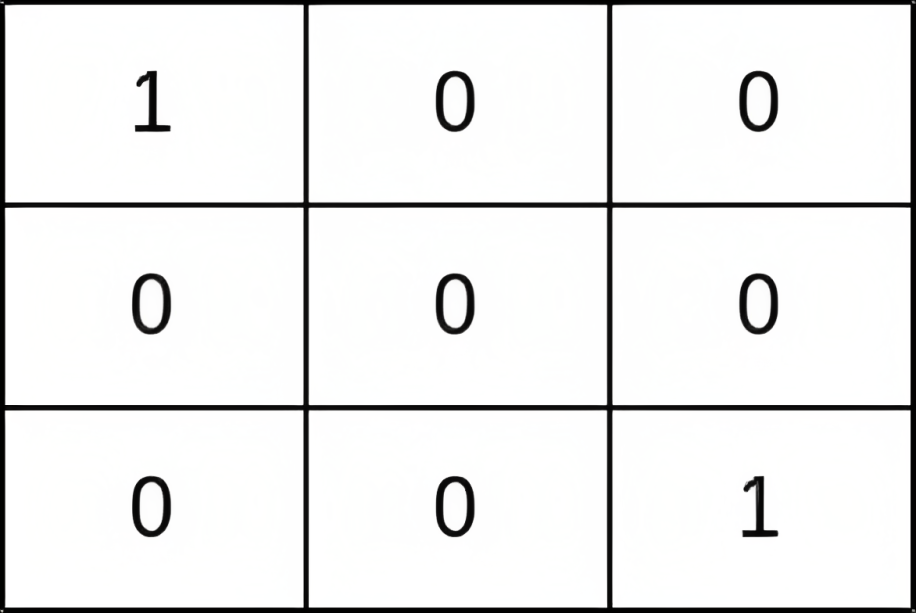
Input: grid = [[1,0,0],[0,0,0],[0,0,1]]
Output: 0
Explanation: All paths from (0, 0) to (n - 1, n - 1) go through the thieves in cells (0, 0) and (n - 1, n - 1).

Example 2:

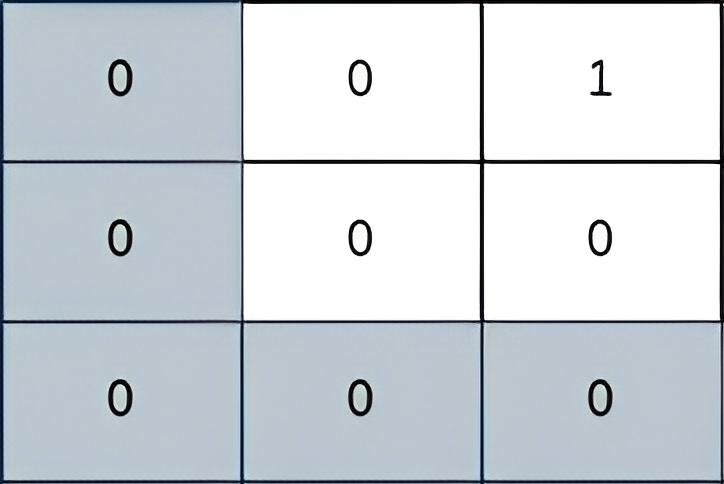
Input: grid = [[0,0,1],[0,0,0],[0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 2) is cell (0, 0). The distance between them is | 0 - 0 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Example 3:

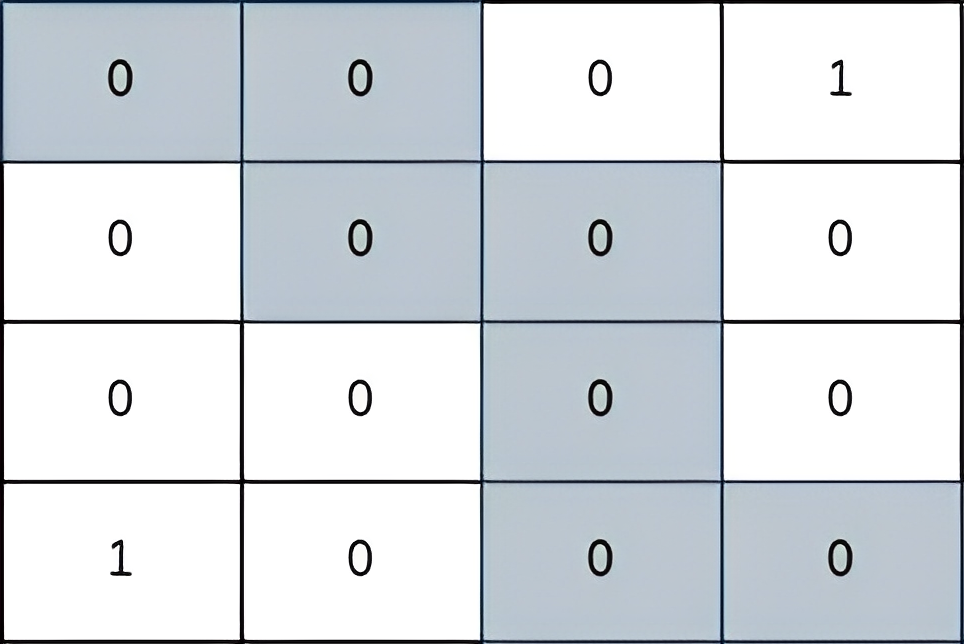
Input: grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 3) is cell (1, 2). The distance between them is | 0 - 1 | + | 3 - 2 | = 2.
- The closest cell of the path to the thief at cell (3, 0) is cell (3, 2). The distance between them is | 3 - 3 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Constraints:

1 <= grid.length == n <= 400
grid[i].length == n
grid[i][j] is either 0 or 1.
There is at least one thief in the grid.

Solution¶

class Solution {
    private int min[][];
    private static int dir[][] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    static class State {
        int row, col, pRow, pCol;
        public State(int row, int col, int pRow, int pCol) {
            this.row = row;
            this.col = col;
            this.pRow = pRow;
            this.pCol = pCol;
        }
        @Override
        public String toString() {
            return "(" + row + " " + col + " " + pRow + " " + pCol + ")";
        }
    }
    static class Tuple {
        int row, col, cost;
        public Tuple(int row, int col, int cost) {
            this.row = row;
            this.col = col;
            this.cost = cost;
        }
        @Override
        public String toString() {
            return "(" + row + " " + col + " " + cost + ")";
        }
    }
    static class customSort implements Comparator<Tuple> {
        @Override
        public int compare(Tuple first, Tuple second) {
            return Integer.compare(second.cost, first.cost);
        }
    }
    public int maximumSafenessFactor(List<List<Integer>> grid) {
        int n = grid.size(), m = grid.get(0).size();
        /* How can we find the closest or minimum hamming distance wala thief for each cell ? */
        min = new int [n][m];
        for (int curr[] : min)
            Arrays.fill(curr, (int)(1e9));
        Queue<State> q = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid.get(i).get(j) == 1) {
                    q.offer(new State(i, j, i, j));
                    min[i][j] = 0;
                }
            }
        }
        while (q.size() > 0) {
            int currRow = q.peek().row, currCol = q.peek().col, pRow = q.peek().pRow, pCol = q.peek().pCol;
            q.poll();
            for (int dire[] : dir) {
                int newRow = currRow + dire[0], newCol = currCol + dire[1];
                if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) {
                    int newDist = Math.abs(pRow - newRow) + Math.abs(pCol - newCol);
                    if (min[newRow][newCol] > newDist) {
                        min[newRow][newCol] = newDist;
                        q.offer(new State(newRow, newCol, pRow, pCol));
                    }
                }
            }
        }
        int low = 0, high = (int)(1e9), ans = -1;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (ok(mid, grid)) {
                ans = mid;
                low = mid + 1;
            }
            else 
                high = mid - 1;
        }
        return ans;
    }
    private boolean ok(int target, List<List<Integer>> arr) {
        int n = arr.size(), m = arr.get(0).size();
        if (min[0][0] < target) return false;
        PriorityQueue<Tuple> pq = new PriorityQueue<>(new customSort());
        int dist[][] = new int[n][m];
        for (int curr[] : dist) 
            Arrays.fill(curr, (int)(-1e9));
        dist[0][0] = min[0][0];
        pq.offer(new Tuple(0, 0, min[0][0]));
        while (pq.size() > 0) {
            int currRow = pq.peek().row, currCol = pq.peek().col, currCost = pq.peek().cost;
            pq.poll();
            if (currRow == n - 1 && currCol == m - 1) 
                return true;
            for (int dire[] : dir) {
                int newRow = currRow + dire[0], newCol = currCol + dire[1];
                if (newRow >= 0 && newCol >= 0 && newRow < n && newCol < m) {
                    if (dist[newRow][newCol] < Math.min(min[newRow][newCol], currCost)) {
                        if (Math.min(min[newRow][newCol], currCost) >= target) {
                            dist[newRow][newCol] = Math.min(min[newRow][newCol], currCost);
                            pq.offer(new Tuple(newRow, newCol, dist[newRow][newCol]));
                        }
                    }
                }
            }
        }
        return false;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here