2793. Count The Number Of Complete Components¶

Difficulty: Medium

2793. Count the Number of Complete Components

Medium

You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting vertices a_i and b_i.

Return the number of complete connected components of the graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

A connected component is said to be complete if there exists an edge between every pair of its vertices.

Example 1:

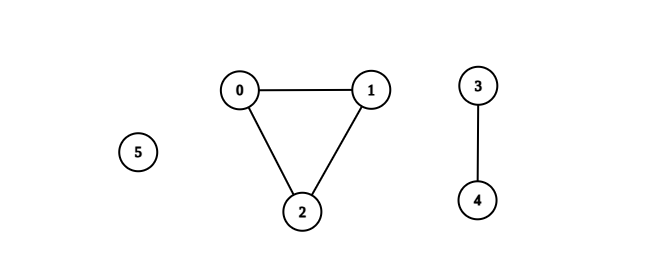
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
Output: 3
Explanation: From the picture above, one can see that all of the components of this graph are complete.

Example 2:

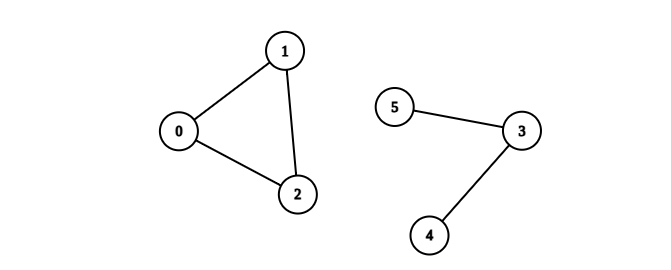
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
Output: 1
Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.

Constraints:

1 <= n <= 50
0 <= edges.length <= n * (n - 1) / 2
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no repeated edges.

Solution¶

class Solution {
    public int countCompleteComponents(int n, int[][] edges) {
        ArrayList<ArrayList<Integer>> adj = new ArrayList<>();
        for (int i = 0; i <= n + 1; i++) adj.add(new ArrayList<>());
        for (int current[] : edges) {
            int u = current[0], v = current[1];
            adj.get(u).add(v);
            adj.get(v).add(u);
        }
        int vis[] = new int[n + 1];
        int count = 0;
        for (int i = 0; i < n; i++) {
            if (vis[i] == 0) {
                ArrayList<Integer> temp = new ArrayList<>();
                dfs(i,adj,vis,temp);
                if (temp.size() == 1) count++;
                else {
                    boolean flag = true;
                    for (int l = 0; l < temp.size(); l++) {
                        int current = temp.get(l), p = adj.get(current).size();
                        if (p != temp.size() - 1) {
                            flag = false;
                            break;
                        }
                    }
                    if (flag == true) count++;
                }
            }
        }
        return count;
    }
    public static void dfs(int u, ArrayList<ArrayList<Integer>> adj, int vis[], ArrayList<Integer> res) {
        vis[u] = 1;
        res.add(u);
        for (int child : adj.get(u)) {
            if (vis[child] == 0) dfs(child, adj, vis, res);
        }
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here