2764. Maximum Number Of Fish In A Grid¶

Difficulty: Medium

2764. Maximum Number of Fish in a Grid

Medium

You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:

A land cell if grid[r][c] = 0, or
A water cell containing grid[r][c] fish, if grid[r][c] > 0.

A fisher can start at any water cell (r, c) and can do the following operations any number of times:

Catch all the fish at cell (r, c), or
Move to any adjacent water cell.

Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.

An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.

Example 1:

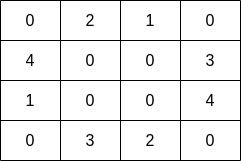
Input: grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
Output: 7
Explanation: The fisher can start at cell (1,3) and collect 3 fish, then move to cell (2,3) and collect 4 fish.

Example 2:

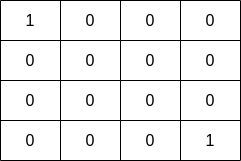
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
Output: 1
Explanation: The fisher can start at cells (0,0) or (3,3) and collect a single fish.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10
0 <= grid[i][j] <= 10

Solution¶

class Solution {
    private int vis[][];
    static class Pair {
        int row, col;
        public Pair(int row, int col) {
            this.row = row;
            this.col = col;
        }
        @Override
        public String toString() {
            return "(" + row + " " + col + ")";
        }
    }
    public int findMaxFish(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        vis = new int[n][m];

        int maxi = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (vis[i][j] == 0 && grid[i][j] > 0) {
                    int currFish = BFS(i, j, grid);
                    maxi = Math.max(maxi, currFish);
                }
            }
        }
        return maxi;
    }

    private int BFS(int row, int col, int arr[][]) {
        int n = arr.length, m = arr[0].length;
        int totalFish = 0;
        vis[row][col] = 1;
        Queue<Pair> q = new LinkedList<>();
        q.offer(new Pair(row, col));
        int dir[][] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        while (q.size() > 0) {
            int currRow = q.peek().row, currCol = q.peek().col;
            q.poll();
            totalFish += arr[currRow][currCol];
            for (int dire[] : dir) {
                int newRow = currRow + dire[0], newCol = currCol + dire[1];
                if (newRow < n && newCol < m && newRow >= 0 && newCol >= 0 && vis[newRow][newCol] == 0 && arr[newRow][newCol] > 0) {
                    vis[newRow][newCol] = 1;
                    q.offer(new Pair(newRow, newCol));
                }
            }
        }
        return totalFish;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here