2583. Divide Nodes Into The Maximum Number Of Groups¶

Difficulty: Hard

2583. Divide Nodes Into the Maximum Number of Groups

Hard

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [a_i,b_i] indicates that there is a bidirectional edge between nodes a_i and b_i. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

Each node in the graph belongs to exactly one group.
For every pair of nodes in the graph that are connected by an edge [a_i,b_i], if a_i belongs to the group with index x, and b_i belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

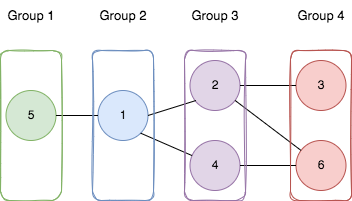
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

Constraints:

1 <= n <= 500
1 <= edges.length <= 10⁴
edges[i].length == 2
1 <= a_i, b_i <= n
a_i != b_i
There is at most one edge between any pair of vertices.

Solution¶

import java.util.*;

class Solution {
    private int[] color; 
    private List<List<Integer>> adj;
    private int n; 
    private boolean isBipartite(int node, int c, List<Integer> component) {
        color[node] = c;
        component.add(node);
        for (int nbr : adj.get(node)) {
            if (color[nbr] == c) return false; 
            if (color[nbr] == -1 && !isBipartite(nbr, 1 - c, component)) 
                return false;
        }
        return true;
    }
    private int maxGroupsInComponent(List<Integer> component) {
        int maxDepth = 0;
        for (int start : component) {
            int[] depth = new int[n];
            Arrays.fill(depth, -1);
            Queue<Integer> q = new LinkedList<>();
            q.add(start);
            depth[start] = 0;
            while (!q.isEmpty()) {
                int node = q.poll();
                for (int nbr : adj.get(node)) {
                    if (depth[nbr] == -1) {
                        depth[nbr] = depth[node] + 1;
                        maxDepth = Math.max(maxDepth, depth[nbr]);
                        q.add(nbr);
                    }
                }
            }
        }
        return maxDepth + 1;
    }
    public int magnificentSets(int n, int[][] edges) {
        this.n = n;
        color = new int[n];
        Arrays.fill(color, -1);
        adj = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            adj.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            int u = edge[0] - 1, v = edge[1] - 1;
            adj.get(u).add(v);
            adj.get(v).add(u);
        }
        List<List<Integer>> components = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (color[i] == -1) {
                List<Integer> component = new ArrayList<>();
                if (!isBipartite(i, 0, component)) 
                    return -1; 
                components.add(component);
            }
        }
        int total = 0;
        for (List<Integer> comp : components) {
            total += maxGroupsInComponent(comp);
        }
        return total;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here