2558. Minimum Number Of Operations To Sort A Binary Tree By Level¶
Difficulty: Medium
LeetCode Problem View on GitHub
2558. Minimum Number of Operations to Sort a Binary Tree by Level
Medium
You are given the root of a binary tree with unique values.
In one operation, you can choose any two nodes at the same level and swap their values.
Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
The level of a node is the number of edges along the path between it and the root node.
Example 1:
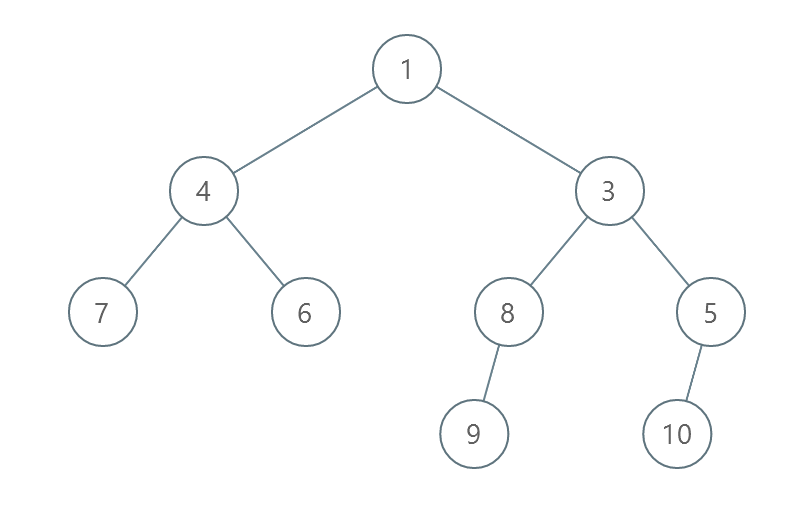
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10] Output: 3 Explanation: - Swap 4 and 3. The 2nd level becomes [3,4]. - Swap 7 and 5. The 3rd level becomes [5,6,8,7]. - Swap 8 and 7. The 3rd level becomes [5,6,7,8]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 2:
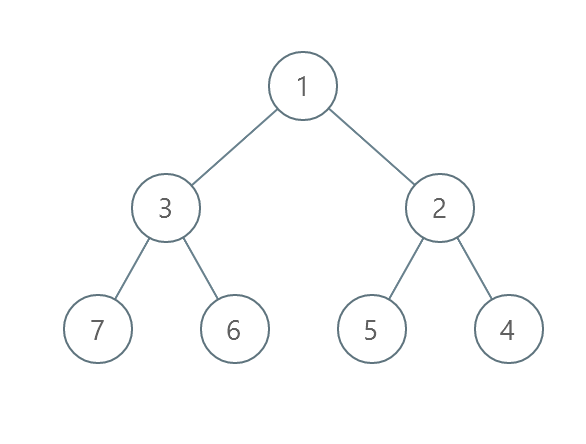
Input: root = [1,3,2,7,6,5,4] Output: 3 Explanation: - Swap 3 and 2. The 2nd level becomes [2,3]. - Swap 7 and 4. The 3rd level becomes [4,6,5,7]. - Swap 6 and 5. The 3rd level becomes [4,5,6,7]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 3:
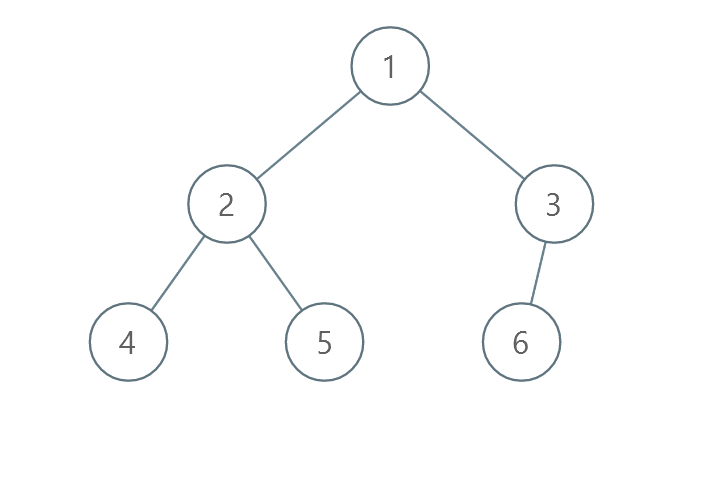
Input: root = [1,2,3,4,5,6] Output: 0 Explanation: Each level is already sorted in increasing order so return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- All the values of the tree are unique.
Solution¶
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minimumOperations(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int res = 0;
while(!q.isEmpty()) {
int len = q.size();
int ans[] = new int[len];
int k = 0;
for(int i = 0; i < len; i++) {
if(q.peek().left != null) q.offer(q.peek().left);
if(q.peek().right != null) q.offer(q.peek().right);
ans[k++] = q.poll().val;
}
res += find(ans);
}
return res;
}
public static int find(int arr[]) {
int n = arr.length;
int temp[] = new int[n];
for(int i = 0; i < n; i++) temp[i] = arr[i];
Arrays.sort(temp);
int count = 0;
for(int i = 0; i < n; i++) {
if(temp[i] != arr[i]) {
count++;
swap(arr, i, index(arr, temp[i]));
}
}
return count;
}
private static int index(int arr[],int ele) {
int n = arr.length;
for(int i = 0; i < n; i++) {
if(arr[i] == ele) return i;
}
return -1;
}
private static void swap(int arr[],int i ,int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here