2531. Create Components With Same Value¶

Difficulty: Hard

2531. Create Components With Same Value

Hard

There is an undirected tree with n nodes labeled from 0 to n - 1.

You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the i^th node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

You are allowed to delete some edges, splitting the tree into multiple connected components. Let the value of a component be the sum of all nums[i] for which node i is in the component.

Return the maximum number of edges you can delete, such that every connected component in the tree has the same value.

Example 1:

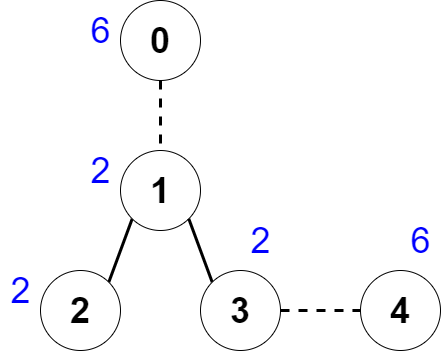
Input: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]] 
Output: 2 
Explanation: The above figure shows how we can delete the edges [0,1] and [3,4]. The created components are nodes [0], [1,2,3] and [4]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.

Example 2:

Input: nums = [2], edges = []
Output: 0
Explanation: There are no edges to be deleted.

Constraints:

1 <= n <= 2 * 10⁴
nums.length == n
1 <= nums[i] <= 50
edges.length == n - 1
edges[i].length == 2
0 <= edges[i][0], edges[i][1] <= n - 1
edges represents a valid tree.

Solution¶

class Solution {
    private ArrayList<ArrayList<Integer>> adj;
    private int count;
    private int val[];
    private int dp[];
    public int componentValue(int[] nums, int[][] edges) {
        int n = nums.length;
        adj = new ArrayList<>();
        for (int i = 0; i <= n + 1; i++)
            adj.add(new ArrayList<>());
        for (int edge[] : edges) {
            int u = edge[0], v = edge[1];
            adj.get(u).add(v);
            adj.get(v).add(u);
        }

        val = new int[n];
        dp = new int[n + 1];
        int start = 0, sum = 0;
        for (int i = 0; i < n; i++) {
            val[i] = nums[i];
            sum += val[i];
            start = Math.max(start, val[i]);
        }

        count = 0;
        int maxi = 0;

        ArrayList<Integer> divs = new ArrayList<>();
        divs = getDivs(sum);

        for (int x = 0; x < divs.size(); x++) {
            int i = divs.get(x);
            dp = new int[n + 1];
            dfs(0, -1, i);
            if (dp[0] == 0) {
                maxi = Math.max(maxi, count - 1);
            }
            count = 0;
        }
        return maxi;
    }
    private void dfs(int u, int par, int req) {
        if (adj.get(u).size() == 1 && u != 0) {
            if (val[u] == req) {
                dp[u] = 0;
                count++;
            }
            else if (val[u] > req) {
                dp[u] = (int)(1e3);
            }
            else dp[u] = val[u];
            return;
        }
        for (int v : adj.get(u)) {
            if (v != par) {
                dfs(v, u, req);
            }
        }
        for (int v : adj.get(u)) {
            if (v != par) {
                dp[u] += dp[v];
            }
        }
        dp[u] += val[u];
        if (dp[u] == req) {
            count++;
            dp[u] = 0;
        }
        else if (dp[u] > req) {
            dp[u] = (int)(1e3);
        }
    }
    private ArrayList<Integer> getDivs(int n) {
        ArrayList<Integer> res = new ArrayList<>();
        for (int i = 1; i * i <= n; i++) {
            if (n % i == 0) {
                res.add(i);
                if (n / i != i) {
                    res.add(n / i);
                } 
            }
        }
        return res;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here