2343. Count Unguarded Cells In The Grid¶
Difficulty: Medium
LeetCode Problem View on GitHub
2343. Count Unguarded Cells in the Grid
Medium
You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.
A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.
Return the number of unoccupied cells that are not guarded.
Example 1:
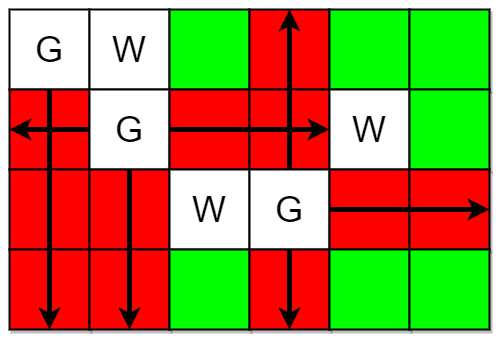
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]] Output: 7 Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram. There are a total of 7 unguarded cells, so we return 7.
Example 2:
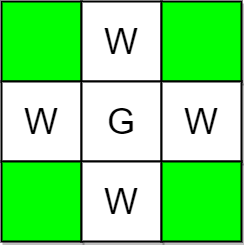
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]] Output: 4 Explanation: The unguarded cells are shown in green in the above diagram. There are a total of 4 unguarded cells, so we return 4.
Constraints:
1 <= m, n <= 1052 <= m * n <= 1051 <= guards.length, walls.length <= 5 * 1042 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < n- All the positions in
guardsandwallsare unique.
Solution¶
class Solution {
static class Pair {
int row, col;
public Pair(int row, int col) {
this.row = row;
this.col = col;
}
@Override
public String toString() {
return "(" + row + " " + col + ")";
}
@Override
public boolean equals(Object obj) {
if (this == obj) return true;
if (obj == null || getClass() != obj.getClass()) return false;
Pair current = (Pair)(obj);
return current.row == row && current.col == col;
}
@Override
public int hashCode() {
return Objects.hash(row, col);
}
}
private HashSet<Pair> bad_cell;
private HashSet<Pair> wall;
private HashSet<Pair> guard;
public int countUnguarded(int n, int m, int[][] guards, int[][] walls) {
bad_cell = new HashSet<>();
wall = new HashSet<>();
guard = new HashSet<>();
for (int curr[] : guards) guard.add(new Pair(curr[0], curr[1]));
for (int curr[] : walls) wall.add(new Pair(curr[0], curr[1]));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (guard.contains(new Pair(i, j))) fill_bad(i, j, n, m);
}
}
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!wall.contains(new Pair(i, j)) && !bad_cell.contains(new Pair(i, j)) && !guard.contains(new Pair(i, j))) {
count++;
}
}
}
return count;
}
private void fill_bad(int row, int col, int n , int m) {
int cr = row, cc = col;
//up;
cr--;
while (cr >= 0) {
if (!wall.contains(new Pair(cr, cc))) bad_cell.add(new Pair(cr, cc));
else break;
if (guard.contains(new Pair(cr, cc))) break;
cr--;
}
//down
cr = row + 1;
cc = col;
while (cr < n) {
if (!wall.contains(new Pair(cr, cc))) bad_cell.add(new Pair(cr, cc));
else break;
if (guard.contains(new Pair(cr, cc))) break;
cr++;
}
//left;
cr = row;
cc = col - 1;
while (cc >= 0) {
if (!wall.contains(new Pair(cr, cc))) bad_cell.add(new Pair(cr, cc));
else break;
if (guard.contains(new Pair(cr, cc))) break;
cc--;
}
//right;
cr = row;
cc = col + 1;
while (cc < m) {
if (!wall.contains(new Pair(cr, cc))) bad_cell.add(new Pair(cr, cc));
else break;
if (guard.contains(new Pair(cr, cc))) break;
cc++;
}
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here