2090. Number Of Ways To Arrive At Destination¶
Difficulty: Medium
LeetCode Problem View on GitHub
2090. Number of Ways to Arrive at Destination
Medium
You are in a city that consists of n intersections numbered from 0 to n - 1 with bi-directional roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer n and a 2D integer array roads where roads[i] = [ui, vi, timei] means that there is a road between intersections ui and vi that takes timei minutes to travel. You want to know in how many ways you can travel from intersection 0 to intersection n - 1 in the shortest amount of time.
Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo 109 + 7.
Example 1:
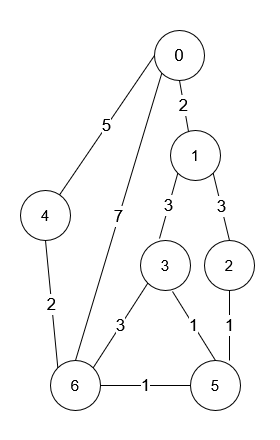
Input: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]] Output: 4 Explanation: The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes. The four ways to get there in 7 minutes are: - 0 â 6 - 0 â 4 â 6 - 0 â 1 â 2 â 5 â 6 - 0 â 1 â 3 â 5 â 6
Example 2:
Input: n = 2, roads = [[1,0,10]] Output: 1 Explanation: There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
Constraints:
1 <= n <= 200n - 1 <= roads.length <= n * (n - 1) / 2roads[i].length == 30 <= ui, vi <= n - 11 <= timei <= 109ui != vi- There is at most one road connecting any two intersections.
- You can reach any intersection from any other intersection.
Solution¶
class Solution {
static class Pair {
long distance;
int node;
public Pair(long distance , int node) {
this.distance = distance;
this.node = node;
}
}
public int countPaths(int n, int[][] roads) {
ArrayList<ArrayList<Pair>> adj = new ArrayList<>();
for(int i = 0; i <= n + 1; i++) adj.add(new ArrayList<>());
for(int current[] : roads) {
int u = current[0];
int v = current[1];
long dist = (long)current[2];
adj.get(u).add(new Pair(dist,v));
adj.get(v).add(new Pair(dist,u));
}
int res = solve(adj,n);
return res;
}
public static int solve(ArrayList<ArrayList<Pair>> adj,int n) {
PriorityQueue<Pair> pq = new PriorityQueue<Pair>((x,y) -> (int)x.distance - (int)y.distance);
long dist[] = new long[n + 1];
Arrays.fill(dist, (long)(1e18));
int ways[] = new int[n + 1];
Arrays.fill(ways,0);
ways[0] = 1;
dist[0] = 0;
pq.offer(new Pair(0,0));
while(!pq.isEmpty()) {
int curr_node = pq.peek().node;
long curr_dist = (long)pq.peek().distance;
pq.poll();
for(int i = 0; i < adj.get(curr_node).size(); i++) {
int child_node = adj.get(curr_node).get(i).node;
long child_dist = (long)adj.get(curr_node).get(i).distance;
if(dist[child_node] > (long)(curr_dist + child_dist)) {
dist[child_node] = (long)(curr_dist + child_dist);
ways[child_node] = ways[curr_node];
pq.offer(new Pair(dist[child_node] , child_node));
}
else if(dist[child_node] == (long)(curr_dist + child_dist)) {
ways[child_node] = (ways[child_node] + ways[curr_node]) % ((int)(1e9 + 7));
}
}
}
return ways[n - 1];
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here