1740. Count Subtrees With Max Distance Between Cities¶

Difficulty: Hard

1740. Count Subtrees With Max Distance Between Cities

Hard

There are n cities numbered from 1 to n. You are given an array edges of size n-1, where edges[i] = [u_i, v_i] represents a bidirectional edge between cities u_i and v_i. There exists a unique path between each pair of cities. In other words, the cities form a tree.

A subtree is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.

For each d from 1 to n-1, find the number of subtrees in which the maximum distance between any two cities in the subtree is equal to d.

Return an array of size n-1 where the d^th element (1-indexed) is the number of subtrees in which the maximum distance between any two cities is equal to d.

Notice that the distance between the two cities is the number of edges in the path between them.

Example 1:

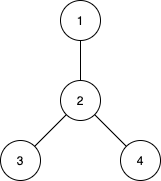
Input: n = 4, edges = [[1,2],[2,3],[2,4]]
Output: [3,4,0]
Explanation:
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.

Example 2:

Input: n = 2, edges = [[1,2]]
Output: [1]

Example 3:

Input: n = 3, edges = [[1,2],[2,3]]
Output: [2,1]

Constraints:

2 <= n <= 15
edges.length == n-1
edges[i].length == 2
1 <= u_i, v_i <= n
All pairs (u_i, v_i) are distinct.

Solution¶

class Solution {
    private ArrayList<ArrayList<Integer>> adj;
    private int arr[];
    private ArrayList<ArrayList<Integer>> subsets;
    private int dp[][];
    private int depth[];

    public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
        adj = new ArrayList<>();
        for (int i = 0; i <= n + 1; i++)
            adj.add(new ArrayList<>());
        for (int edge[] : edges) {
            int u = edge[0], v = edge[1];
            adj.get(u).add(v);
            adj.get(v).add(u);
        }
        arr = new int[n];
        for (int i = 0; i < n; i++)
            arr[i] = i + 1;
        subsets = new ArrayList<>();

        getSubsets(0, arr, new ArrayList<>());

        dp = new int[n + 1][19];
        depth = new int[n + 1];
        dfs(1, 0);

        int res[] = new int[n - 1];
        for (ArrayList<Integer> curr : subsets) {
            int maxi = 0, count = 0;
            for (int i = 0; i < curr.size(); i++) {
                for (int j = i + 1; j < curr.size(); j++) {
                    int u = curr.get(i), v = curr.get(j);
                    if (adj.get(u).contains(v)) count++;
                    int dist = depth[u] + depth[v] - 2 * depth[lca(u, v)];
                    maxi = Math.max(maxi, dist);
                }
            }
            if (count == curr.size() - 1 && maxi > 0) res[maxi - 1]++;
        }
        return res;
    }

    private void dfs(int u, int par) {
        dp[u][0] = par;
        for (int i = 1; i < 19; i++)
            dp[u][i] = dp[dp[u][i - 1]][i - 1];
        for (int v : adj.get(u)) {
            if (v != par) {
                depth[v] = 1 + depth[u];
                dfs(v, u);
            }
        }
    }

    private int lca(int u, int v) {
        if (depth[u] > depth[v]) {
            int temp = u;
            u =  v;
            v = temp;
        }
        int diff = depth[v] - depth[u];
        v = kthParent(v, diff);
        if (u == v)
            return u;
        for (int i = 18; i >= 0; i--) {
            if (dp[u][i] != dp[v][i]) {
                u = dp[u][i];
                v = dp[v][i];
            }
        }
        return dp[u][0];
    }

    private int kthParent(int u, int k) {
        int count = 0;
        while (k > 0) {
            if (k % 2 == 1) 
                u = dp[u][count];
            count++;
            k >>= 1;
        }
        return u;
    }

    private void getSubsets(int ind, int arr[], ArrayList<Integer> current) {
        if (ind >= arr.length) {
            if (current.size() <= 1) return;
            subsets.add(new ArrayList<>(current));
            return;
        }

        current.add(arr[ind]);
        getSubsets(ind + 1, arr, current);
        current.remove(current.size() - 1);
        getSubsets(ind + 1, arr, current);
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here