1653. Number Of Good Leaf Nodes Pairs¶
Difficulty: Medium
LeetCode Problem View on GitHub
1653. Number of Good Leaf Nodes Pairs
Medium
You are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.
Return the number of good leaf node pairs in the tree.
Example 1:
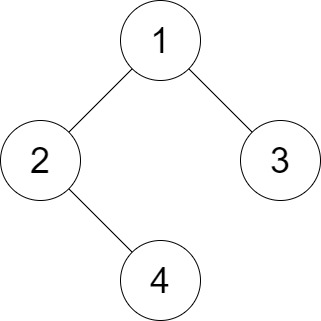
Input: root = [1,2,3,null,4], distance = 3 Output: 1 Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
Example 2:
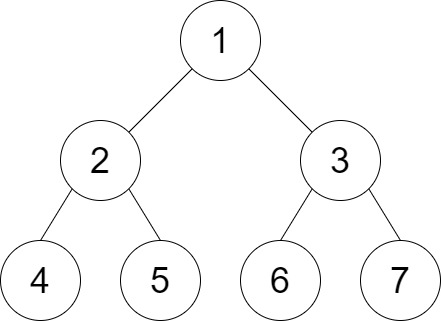
Input: root = [1,2,3,4,5,6,7], distance = 3 Output: 2 Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.
Example 3:
Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3 Output: 1 Explanation: The only good pair is [2,5].
Constraints:
- The number of nodes in the
treeis in the range[1, 210]. 1 <= Node.val <= 1001 <= distance <= 10
Solution¶
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countPairs(TreeNode root, int distance) {
ArrayList<ArrayList<Integer>> adj = new ArrayList<>();
HashMap<TreeNode , Integer> id = new HashMap<>();
for(int i = 0; i <= 2000; i++) adj.add(new ArrayList<>());
int current_id = 0;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while(q.size() > 0) {
int len = q.size();
if(!id.containsKey(q.peek())) {
id.put(q.peek(), current_id);
current_id++;
}
for(int i = 0; i < len; i++) {
if(q.peek().left != null) {
if(!id.containsKey(q.peek().left)) {
id.put(q.peek().left, current_id);
current_id++;
adj.get(id.get(q.peek())).add(id.get(q.peek().left));
adj.get(id.get(q.peek().left)).add(id.get(q.peek()));
q.offer(q.peek().left);
}
}
if(q.peek().right != null) {
if(!id.containsKey(q.peek().right)) {
id.put(q.peek().right, current_id);
current_id++;
adj.get(id.get(q.peek())).add(id.get(q.peek().right));
adj.get(id.get(q.peek().right)).add(id.get(q.peek()));
q.offer(q.peek().right);
}
}
q.poll();
}
}
ArrayList<Integer> leaf = new ArrayList<>();
for(int i = 0; i <= current_id; i++) {
if(adj.get(i).size() == 1 && i != id.get(root)) {
leaf.add(i);
}
}
int dp[][] = new int[2000 + 1][18];
int depth[] = new int[2000 + 1];
dfs(0, 0, adj, dp, depth);
int count = 0;
for(int i = 0; i < leaf.size(); i++) {
int u = leaf.get(i);
for(int j = i + 1; j < leaf.size(); j++) {
int v = leaf.get(j);
int dist = depth[u] + depth[v] - 2 * depth[lca(u , v, depth, dp)];
if(dist <= distance) count++;
}
}
return count;
}
public static void dfs(int u , int par, ArrayList<ArrayList<Integer>> adj , int dp[][], int depth[]) {
dp[u][0] = par;
for(int i = 1; i <= 17; i++) {
dp[u][i] = dp[dp[u][i - 1]][i - 1];
}
for(int v : adj.get(u)) {
if(v != par) {
depth[v] = 1 + depth[u];
dfs(v, u, adj ,dp, depth);
}
}
}
public static int find_kth_parent(int u , int k , int dp[][]) {
int count = 0;
while(k != 0) {
if(k % 2 == 1) {
u = dp[u][count];
}
count++;
k = k >> 1;
}
return u;
}
public static int lca(int node1 , int node2,int depth[] , int dp[][]) {
if(depth[node1] > depth[node2]) {
int temp = node1;
node1 = node2;
node2 = temp;
}
int diff = depth[node2] - depth[node1];
node2 = find_kth_parent(node2 , diff, dp);
if(node1 == node2) return node1;
for(int i = 17; i >= 0; i--) {
if(dp[node1][i] != dp[node2][i]) {
node1 = dp[node1][i];
node2 = dp[node2][i];
}
}
return dp[node1][0];
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here