1628. Count Submatrices With All Ones¶

Difficulty: Medium

1628. Count Submatrices With All Ones

Medium

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

Example 1:

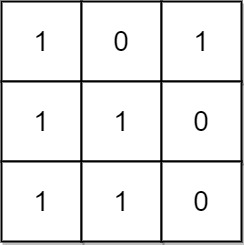
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]
Output: 13
Explanation: 
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2. 
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

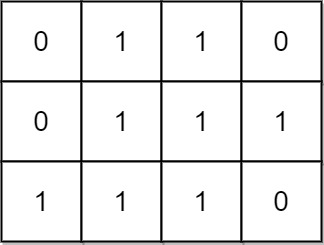
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
Output: 24
Explanation: 
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3. 
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2. 
There are 2 rectangles of side 3x1. 
There is 1 rectangle of side 3x2. 
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

Constraints:

1 <= m, n <= 150
mat[i][j] is either 0 or 1.

Solution¶

class Solution {
    static class Pair {
        int val;
        int index;
        public Pair(int val, int index) {
            this.val = val;
            this.index = index;
        }
        @Override
        public String toString() {
            return "(" + val + " " + index + ")";
        }
    }
    public int numSubmat(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        int current_state[] = new int[m];
        int res = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (mat[i][j] == 0) current_state[j] = 0;
                else current_state[j]++;
            }
            res += find_sum_of_all_heights_of_histogram(current_state);
        }
        return res;
    }

    private int find_sum_of_all_heights_of_histogram(int arr[]) {
        int n = arr.length;
        Stack<Pair> st = new Stack<>();
        int prev_smallest[] = new int[n];
        int next_smallest[] = new int[n];

        for (int i = 0; i < n; i++) {
            int current = arr[i];
            while (st.size() > 0 && st.peek().val >= current) st.pop();
            if (st.size() == 0) prev_smallest[i] = -1;
            else prev_smallest[i] = st.peek().index;
            st.add(new Pair(current, i));
        }
        st.clear();

        for (int i = n - 1; i >= 0; i--) {
            int current = arr[i];
            while (st.size() > 0 && st.peek().val >= current) st.pop();
            if (st.size() == 0) next_smallest[i] = -1;
            else next_smallest[i] = st.peek().index;
            st.add(new Pair(current, i));
        }

        int res[] = new int[n];
        for (int i = 0; i < n; i++) {
            int current = arr[i];
            int next_smaller_index = next_smallest[i];
            int prev_smaller_index = prev_smallest[i];
            if (prev_smaller_index == -1) res[i] = current * (i + 1);
            else {
                res[i] = res[prev_smaller_index];
                res[i] += current * (i - prev_smaller_index);
            }
        }
        int total = 0;
        for (int ele : res) total += ele;
        return total;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here