1558. Course Schedule Iv¶

Difficulty: Medium

1558. Course Schedule IV

Medium

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [a_i, b_i] indicates that you must take course a_i first if you want to take course b_i.

For example, the pair [0, 1] indicates that you have to take course 0 before you can take course 1.

Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.

You are also given an array queries where queries[j] = [u_j, v_j]. For the j^th query, you should answer whether course u_j is a prerequisite of course v_j or not.

Return a boolean array answer, where answer[j] is the answer to the j^th query.

Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0.
Course 0 is not a prerequisite of course 1, but the opposite is true.

Example 2:

Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites, and each course is independent.

Example 3:

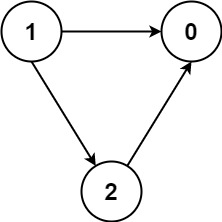
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]

Constraints:

2 <= numCourses <= 100
0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
prerequisites[i].length == 2
0 <= a_i, b_i <= numCourses - 1
a_i != b_i
All the pairs [a_i, b_i] are unique.
The prerequisites graph has no cycles.
1 <= queries.length <= 10⁴
0 <= u_i, v_i <= numCourses - 1
u_i != v_i

Solution¶

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        int[] indegree = new int[n];
        Map<Integer, Set<Integer>> adj = new HashMap<>(); 
        Map<Integer, Set<Integer>> prerequisitesMap = new HashMap<>(); 
        for (int i = 0 ; i < n; i++) {
            prerequisitesMap.put(i, new HashSet<>());
            adj.put(i, new HashSet<>());
        }
        for (int[] pre : prerequisites) {
            indegree[pre[1]]++;
            adj.get(pre[0]).add(pre[1]);
        }
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (indegree[i] == 0) queue.offer(i);
        }
        while (!queue.isEmpty()) {
            int node = queue.poll();            
            Set<Integer> set = adj.get(node);
            for (int next : set) {
                prerequisitesMap.get(next).add(node);
                prerequisitesMap.get(next).addAll(prerequisitesMap.get(node));
                indegree[next]--;
                if (indegree[next] == 0) queue.offer(next);
            }
        }
        List<Boolean> res = new ArrayList<>();
        for (int[] pair : queries) {
            Set<Integer> set = prerequisitesMap.get(pair[1]);
            if (set.contains(pair[0])) res.add(true);
            else res.add(false);
        }
        return res;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here