1485. Minimum Cost To Make At Least One Valid Path In A Grid¶

Difficulty: Hard

1485. Minimum Cost to Make at Least One Valid Path in a Grid

Hard

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

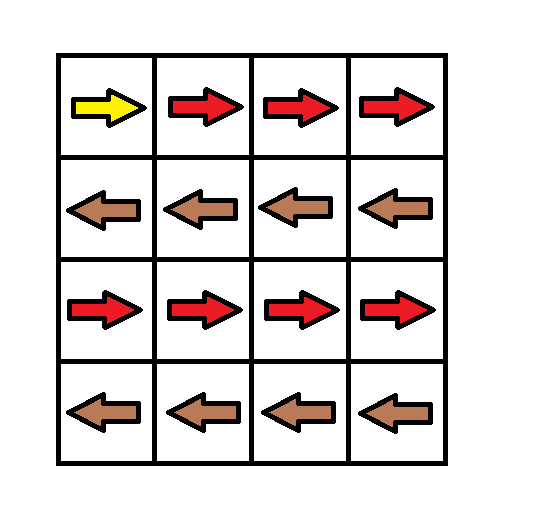
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

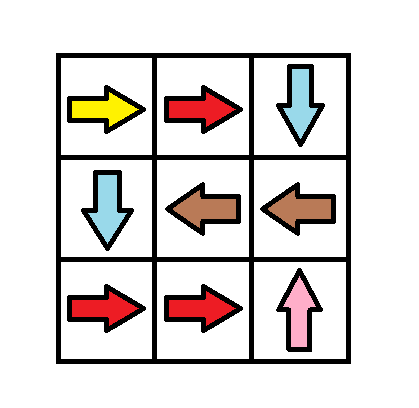
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

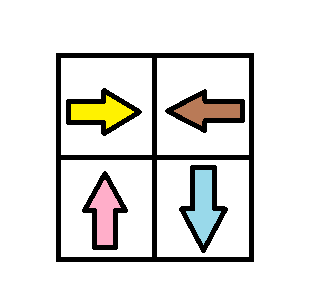
Input: grid = [[1,2],[4,3]]
Output: 1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
1 <= grid[i][j] <= 4

Solution¶

class Solution {
    static class Pair {
        int row, col, val,cost;
        public Pair(int row, int col,int val,int cost) {
            this.row = row;
            this.col = col;
            this.val = val;
            this.cost = cost;
        }
    }
    public int minCost(int[][] grid) {
        return bfs(0, 0, grid);
    }
    public static int bfs(int row, int col, int grid[][]) {
        int n = grid.length;
        int m = grid[0].length;
        int dir[][] = {{-1, 0} , {1, 0} , {0, -1} , {0 , 1}};
        Queue<Pair> q = new LinkedList<>();
        int dist[][] = new int[n + 1][m + 1];
        for(int current[] : dist) Arrays.fill(current, (int)(1e9));
        dist[0][0] = 0;
        q.offer(new Pair(0,0,grid[0][0],0));
        int min = Integer.MAX_VALUE;
        while(!q.isEmpty()) {
            int cr = q.peek().row;
            int cc = q.peek().col;
            int cv = q.peek().val;
            int ccost = q.peek().cost;
            System.out.println(cr + " " + cc + " " + ccost);
            if(cr == n - 1 && cc == m - 1) min = Math.min(min, ccost);
            q.poll();
            if(cv == 1) {
                int nr = cr;
                int nc = cc + 1;
                if(nc < m) {
                    if(dist[nr][nc] > ccost) {
                        q.offer(new Pair(nr, nc, grid[nr][nc] , ccost));
                        dist[nr][nc] = ccost;
                    }
                }
            }
            if(cv == 2) {
                int nr = cr;
                int nc = cc - 1;
                if(nc >= 0) {
                    if(dist[nr][nc] > ccost) {
                        q.offer(new Pair(nr, nc, grid[nr][nc] , ccost));
                        dist[nr][nc] = ccost;
                    }
                }
            }
            if(cv == 3) {
                int nr = cr + 1;
                int nc = cc;
                if(nr < n) {
                    if(dist[nr][nc] > ccost) {
                        q.offer(new Pair(nr, nc, grid[nr][nc] , ccost));
                        dist[nr][nc] = ccost;
                    }
                }
            }
            if(cv == 4) {
                int nr = cr - 1;
                int nc = cc;
                if(nr >= 0) {
                    if(dist[nr][nc] > ccost) {
                        q.offer(new Pair(nr, nc, grid[nr][nc] , ccost));
                        dist[nr][nc] = ccost;
                    }
                }
            }
            for(int dire[] : dir) {
                int nr = cr + dire[0];
                int nc = cc + dire[1];
                if(nr >= 0 && nr < n && nc >= 0 && nc < m) {
                    if(dist[nr][nc] > ccost + 1) {
                        q.offer(new Pair(nr, nc, grid[nr][nc] , ccost + 1));
                        dist[nr][nc] = ccost + 1;
                    }
                }
            }
        }
        return Math.min(min, dist[n - 1][m - 1]);
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here