1409. Minimum Number Of Flips To Convert Binary Matrix To Zero Matrix¶

Difficulty: Hard

1409. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

Hard

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbors of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighbors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

A binary matrix is a matrix with all cells equal to 0 or 1 only.

A zero matrix is a matrix with all cells equal to 0.

Example 1:

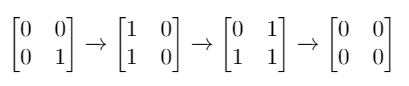
Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We do not need to change it.

Example 3:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix cannot be a zero matrix.

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 3
mat[i][j] is either 0 or 1.

Solution¶

import java.util.ArrayList;

class Solution {
    static class Pair {
        int row, col;
        public Pair(int row, int col) {
            this.row = row;
            this.col = col;
        }
        @Override
        public String toString() {
            return "Pair{" +
                   "row=" + row +
                   ", col=" + col +
                   '}';
        }
    }
    private ArrayList<ArrayList<Pair >> choose;
    public int minFlips(int[][] mat) {
        int n = mat.length, m = mat[0].length;
        choose = new ArrayList<>();

        solve(0, 0, new ArrayList<>(), mat);

        int mini = Integer.MAX_VALUE;
        int dir[][] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        for (ArrayList<Pair> curr : choose) {
            int arr[][] = new int[n][m];
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++)
                    arr[i][j] = mat[i][j];
            }
            for (Pair p : curr) {
                int currRow = p.row, currCol = p.col;
                arr[currRow][currCol] = 1 - arr[currRow][currCol];
                for (int dire[] : dir) {
                    int newRow = currRow + dire[0], newCol = currCol + dire[1];
                    if (newRow >= 0 && newCol >= 0 && newRow < n && newCol < m)
                        arr[newRow][newCol] = 1 - arr[newRow][newCol];
                }
            }
            boolean flag = true;
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    if (arr[i][j] != 0) {
                        flag = false;
                        break;
                    }
                }
                if (flag == false)
                    break;
            }
            if (flag == true)
                mini = Math.min(mini, curr.size());
        }
        if (mini == Integer.MAX_VALUE)
            return -1;
        return mini;
    }

    private void solve(int row, int col, ArrayList<Pair> current, int mat[][]) {
        if (row == mat.length - 1 && col == mat[0].length) {
            choose.add(new ArrayList<>(current));
            return;
        }

        if (row == mat.length && col == mat[0].length) {
            choose.add(new ArrayList<>(current));
            return;
        }

        if (col == mat[0].length) {
            row++;
            col = 0;
        }

        current.add(new Pair(row, col));
        solve(row, col + 1, current, mat);

        current.remove(current.size() - 1);
        solve(row, col + 1, current, mat);
    }

}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here