1342. Queens That Can Attack The King¶

Difficulty: Medium

1342. Queens That Can Attack the King

Medium

On a 0-indexed 8 x 8 chessboard, there can be multiple black queens and one white king.

You are given a 2D integer array queens where queens[i] = [xQueen_i, yQueen_i] represents the position of the i^th black queen on the chessboard. You are also given an integer array king of length 2 where king = [xKing, yKing] represents the position of the white king.

Return the coordinates of the black queens that can directly attack the king. You may return the answer in any order.

Example 1:

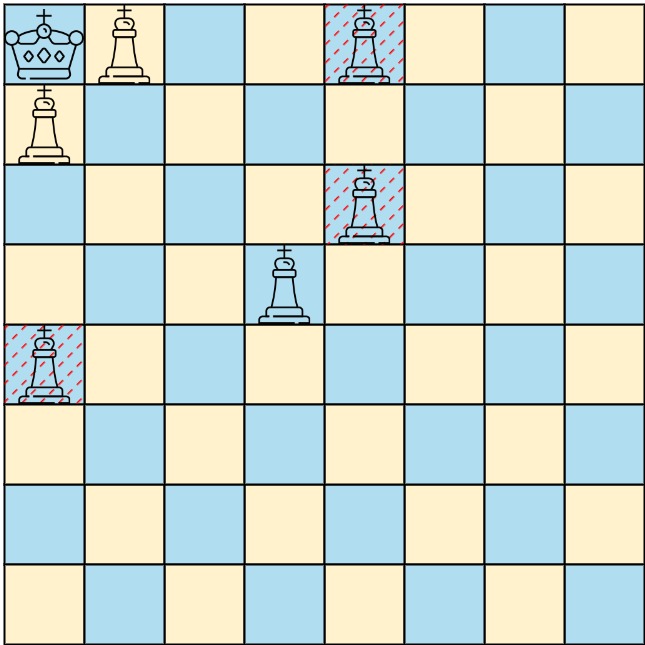
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).

Example 2:

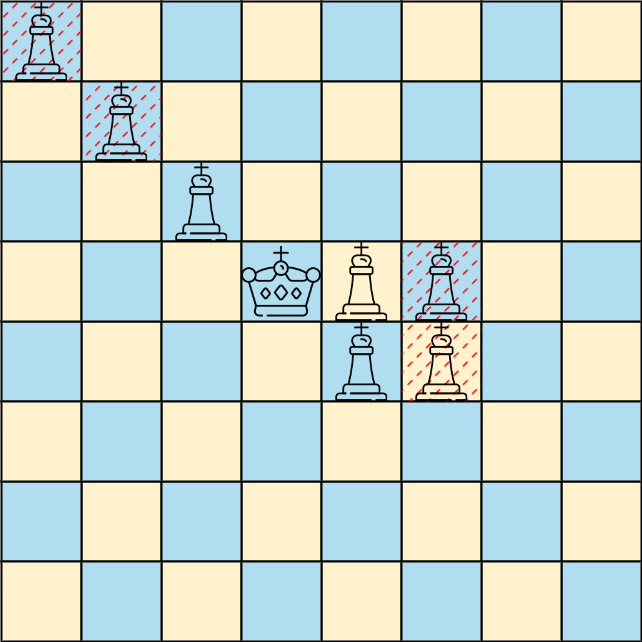
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]
Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).

Constraints:

1 <= queens.length < 64
queens[i].length == king.length == 2
0 <= xQueen_i, yQueen_i, xKing, yKing < 8
All the given positions are unique.

Solution¶

class Solution {
    static HashSet<Pair> set;
    static class Pair {
        int row, col;
        public Pair(int row, int col) {
            this.row = row;
            this.col = col;
        }
        @Override
        public String toString() {
            return "(" + row + " " + col + ")";
        }
        @Override
        public boolean equals(Object obj) {
            if (this == obj) return true;
            if (obj == null || getClass() != obj.getClass()) return false;
            Pair current = (Pair)(obj);
            return current.row == row && current.col == col;
        }
        @Override
        public int hashCode() {
            return Objects.hash(row, col);
        }
    }
    public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
        int n = queens.length;
        List<List<Integer>> res = new ArrayList<>();
        set = new HashSet<>();
        for (int pos[] : queens) set.add(new Pair(pos[0] , pos[1]));
        for (int pos[] : queens) {
            if (can_attack(pos[0] , pos[1] , king[0] , king[1])) {
                List<Integer> temp = new ArrayList<>();
                temp.add(pos[0]); temp.add(pos[1]);
                res.add(new ArrayList<>(temp));
            }
        }
        return res;
    }

    static boolean can_attack(int x, int y , int rx, int ry) {
        int n = 8, m = 8;

        //Right
        int cx = x, cy = y + 1;
        while (cy < m) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cy++;
        }

        //Left
        cx = x; cy = y - 1;
        while (cy >= 0) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cy--;
        }

        //Down
        cx = x + 1; cy = y;
        while (cx < n) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cx++;
        }

        //Up
        cx = x - 1; cy = y;
        while (cx >= 0) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cx--;
        }

        //Right Upper Diagonal        
        cx = x - 1; cy = y + 1;
        while (cx >= 0 && cy < m) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cx--; cy++;
        }

        //Left Upper Diagonal
        cx = x - 1; cy = y - 1;
        while (cx >= 0 && cy >= 0) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cx--; cy--;
        }

        //Lower Left Diagonal
        cx = x + 1; cy = y - 1;
        while (cx < n && cy >= 0) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cx++; cy--;
        }

        //Lower Right Diagonal
        cx = x + 1; cy = y + 1;
        while (cx < n && cy < m) {
            if (set.contains(new Pair(cx , cy))) break;
            if (cx == rx && cy == ry) return true;
            cx++; cy++;
        }
        return false;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here