1145. Number Of Submatrices That Sum To Target¶

Difficulty: Hard

1145. Number of Submatrices That Sum to Target

Hard

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

Example 1:

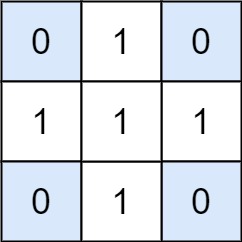
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.

Example 3:

Input: matrix = [[904]], target = 0
Output: 0

Constraints:

1 <= matrix.length <= 100
1 <= matrix[0].length <= 100
-1000 <= matrix[i][j] <= 1000
-10^8 <= target <= 10^8

Solution¶

class Solution {
    private int pref[][];
    public int numSubmatrixSumTarget(int[][] matrix, int target) {
        int n = matrix.length;
        int m = matrix[0].length;

        build(matrix);

        int count = 0;
        for (int x1 = 0; x1 < n; x1++) {
            for (int y1 = 0; y1 < m; y1++) {
                for (int x2 = x1; x2 < n; x2++) {
                    for (int y2 = y1; y2 < m; y2++) {
                        if (query(x1, y1, x2, y2) == target)
                            count++;
                    }
                }
            }
        }
        return count;

    }

    private void build(int arr[][]) {
        int n = arr.length, m = arr[0].length;
        pref = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                pref[i][j] = arr[i][j];
                if (i - 1 >= 0)
                    pref[i][j] += pref[i - 1][j];
                if (j - 1 >= 0)
                    pref[i][j] += pref[i][j - 1];
                if (i - 1 >= 0 && j - 1 >= 0)
                    pref[i][j] -= pref[i - 1][j - 1];
            }
        }
    }

    private int query(int x1, int y1, int x2, int y2) {
        int total = pref[x2][y2];
        if (x1 - 1 >= 0)
            total -= pref[x1 - 1][y2];
        if (y1 - 1 >= 0)
            total -= pref[x2][y1 - 1];
        if (x1 - 1 >= 0 && y1 - 1 >= 0)
            total += pref[x1 - 1][y1 - 1];
        return total;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here