893. All Nodes Distance K In Binary Tree¶
Difficulty: Medium
LeetCode Problem View on GitHub
893. All Nodes Distance K in Binary Tree
Medium
Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
Example 1:
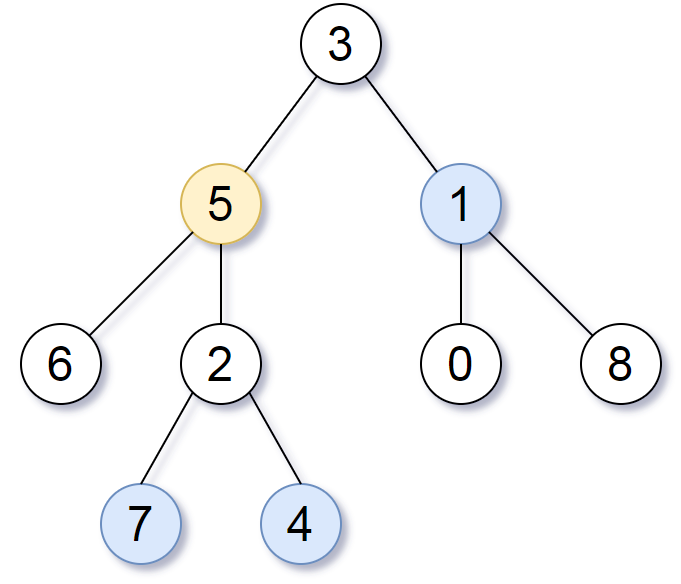
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2 Output: [7,4,1] Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
Example 2:
Input: root = [1], target = 1, k = 3 Output: []
Constraints:
- The number of nodes in the tree is in the range
[1, 500]. 0 <= Node.val <= 500- All the values
Node.valare unique. targetis the value of one of the nodes in the tree.0 <= k <= 1000
Solution¶
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private ArrayList<ArrayList<Integer>> adj;
private HashMap<TreeNode, Integer> getId;
private HashMap<Integer, TreeNode> getNode;
private int id;
public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
adj = new ArrayList<>();
for (int i = 0; i <= (int)(501); i++)
adj.add(new ArrayList<>());
buildTree(root);
int startId = getId.get(target);
List<Integer> res = BFS(startId, k);
return res;
}
private List<Integer> BFS(int start, int k) {
int vis[] = new int[(int)(501)];
int dist[] = new int[(int)(501)];
List<Integer> res = new ArrayList<>();
Queue<Integer> q = new LinkedList<>();
q.offer(start);
vis[start] = 1;
dist[start] = 0;
while (q.size() > 0) {
int currNode = q.peek();
q.poll();
for (int v : adj.get(currNode)) {
if (vis[v] == 0) {
vis[v] = 1;
dist[v] = 1 + dist[currNode];
q.offer(v);
}
}
}
for (int i = 1; i < id; i++) {
if (dist[i] == k) {
res.add(getNode.get(i).val);
}
}
return res;
}
private void buildTree(TreeNode root) {
id = 1;
getId = new HashMap<>();
getNode = new HashMap<>();
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (q.size() > 0) {
int len = q.size();
for (int i = 0; i < len; i++) {
if (!getId.containsKey(q.peek())) {
getId.put(q.peek(), id);
getNode.put(id, q.peek());
id++;
}
if (q.peek().left != null) {
getId.put(q.peek().left, id);
getNode.put(id, q.peek().left);
q.offer(q.peek().left);
id++;
int u = getId.get(q.peek()), v = getId.get(q.peek().left);
adj.get(u).add(v);
adj.get(v).add(u);
}
if (q.peek().right != null) {
getId.put(q.peek().right, id);
getNode.put(id, q.peek().right);
q.offer(q.peek().right);
id++;
int u = getId.get(q.peek()), v = getId.get(q.peek().right);
adj.get(u).add(v);
adj.get(v).add(u);
}
q.poll();
}
}
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here