803. Cheapest Flights Within K Stops¶
Difficulty: Medium
LeetCode Problem View on GitHub
803. Cheapest Flights Within K Stops
Medium
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
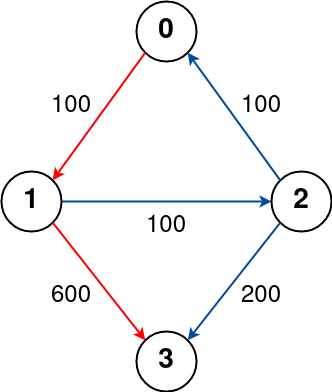
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
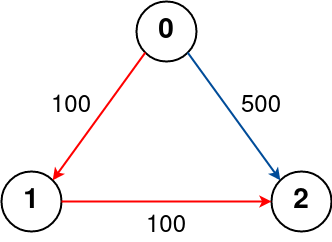
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3:
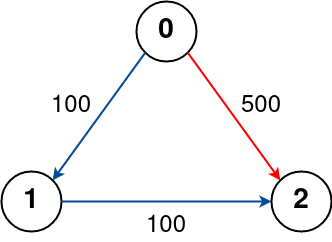
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
Solution¶
class Solution {
private int dist[][];
private ArrayList<ArrayList<Pair>> adj;
static class Pair {
int node, weight;
public Pair(int node, int weight) {
this.node = node;
this.weight = weight;
}
@Override
public String toString() {
return "(" + node + " " + weight + ")";
}
}
static class Tuple {
int node, weight, used;
public Tuple(int node, int weight, int used) {
this.node = node;
this.weight = weight;
this.used = used;
}
@Override
public String toString() {
return "(" + node + " " + weight + " " + used + ")";
}
}
static class customSort implements Comparator<Tuple> {
@Override
public int compare(Tuple first, Tuple second) {
return Integer.compare(first.weight, second.weight);
}
}
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
dist = new int[n + 1][k + 2];
for (int current[] : dist)
Arrays.fill(current, (int)(1e9));
dist[src][0] = 0;
adj = new ArrayList<>();
for (int i = 0; i <= n + 1; i++)
adj.add(new ArrayList<>());
for (int edge[] : flights) {
int u = edge[0], v = edge[1], wt = edge[2];
adj.get(u).add(new Pair(v, wt));
}
PriorityQueue<Tuple> pq = new PriorityQueue<>(new customSort());
pq.offer(new Tuple(src, 0, 0));
while (pq.size() > 0) {
int currNode = pq.peek().node, currCost = pq.peek().weight, currUsed = pq.peek().used;
pq.poll();
for (int i = 0; i < adj.get(currNode).size(); i++) {
int childNode = adj.get(currNode).get(i).node;
int childWeight = adj.get(currNode).get(i).weight;
if (currUsed + 1 > k + 1) continue;
if (dist[childNode][currUsed + 1] > dist[currNode][currUsed] + childWeight) {
dist[childNode][currUsed + 1] = dist[currNode][currUsed] + childWeight;
pq.offer(new Tuple(childNode, dist[childNode][currUsed + 1], currUsed + 1));
}
}
}
int mini = (int)(1e9);
for (int i = 0; i <= k + 1; i++) {
mini = Math.min(mini, dist[dst][i]);
}
if (mini == (int)(1e9))
return -1;
return mini;
}
}
Complexity Analysis¶
- Time Complexity:
O(?) - Space Complexity:
O(?)
Approach¶
Detailed explanation of the approach will be added here