777. Toeplitz Matrix¶

LeetCode Problem View on GitHub

777. Toeplitz Matrix

Easy

Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false.

A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.

Example 1:

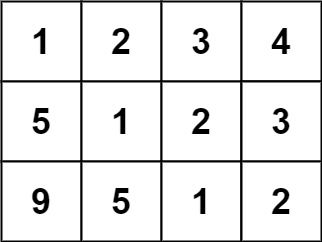
Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
Output: true
Explanation:
In the above grid, the diagonals are:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]".
In each diagonal all elements are the same, so the answer is True.

Example 2:

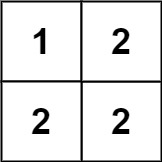
Input: matrix = [[1,2],[2,2]]
Output: false
Explanation:
The diagonal "[1, 2]" has different elements.

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 20
• 0 <= matrix[i][j] <= 99

Follow up:

• What if the matrix is stored on disk, and the memory is limited such that you can only load at most one row of the matrix into the memory at once?
• What if the matrix is so large that you can only load up a partial row into the memory at once?

Solution¶

class Solution {
    public boolean isToeplitzMatrix(int[][] matrix) {
        int n = matrix.length, m = matrix[0].length;
        for (int j = 0; j < m; j++) {
            int startRow = 0, startCol = j;
            while (startRow < n && startCol < m) {
                if (matrix[startRow][startCol] != matrix[0][j]) {
                    return false;
                }
                startRow++;
                startCol++;
            }
        }
        for (int i = 0; i < n; i++) {
            int startRow = i, startCol = 0;
            while (startRow < n && startCol < m) {
                if (matrix[startRow][startCol] != matrix[i][0]) {
                    return false;
                }
                startRow++;
                startCol++;
            }
        }
        return true;
    }
}

Complexity Analysis¶

• Time Complexity: O(?)
• Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here