769. Largest Plus Sign¶

Difficulty: Medium

769. Largest Plus Sign

Medium

You are given an integer n. You have an n x n binary grid grid with all values initially 1's except for some indices given in the array mines. The i^th element of the array mines is defined as mines[i] = [x_i, y_i] where grid[x_i][y_i] == 0.

Return the order of the largest axis-aligned plus sign of 1's contained in grid. If there is none, return 0.

An axis-aligned plus sign of 1's of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1's. Note that there could be 0's or 1's beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1's.

Example 1:

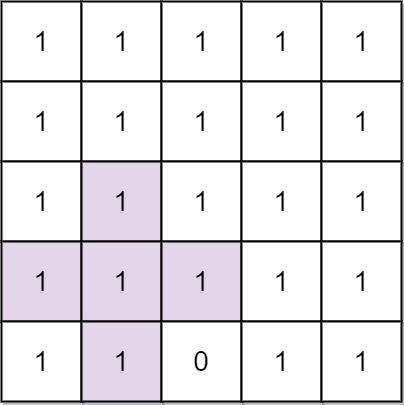
Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.

Example 2:

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.

Constraints:

1 <= n <= 500
1 <= mines.length <= 5000
0 <= x_i, y_i < n
All the pairs (x_i, y_i) are unique.

Solution¶

import java.util.Arrays;

class Solution {
    private int rowPref[][];
    private int colPref[][];
    private int arr[][];
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        rowPref = new int[n + 1][n + 1];
        colPref = new int[n + 1][n + 1];

        arr = new int[n + 1][n + 1];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++)
                arr[i][j] = 1;
        }
        for (int curr[] : mines)
            arr[curr[0]][curr[1]] = 0;

        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = 0; j < n; j++) {
                sum += arr[i][j];
                rowPref[i][j] = sum;
            }
        }

        for (int j = 0; j < n; j++) {
            int sum = 0;
            for (int i = 0; i < n; i++) {
                sum += arr[i][j];
                colPref[j][i] = sum;
            }
        }

        int low = 1, high = n, ans = 0;
        while (low <= high) {
            int mid = low + (high - low) / 2;
            if (ok(mid, n)) {
                ans = mid;
                low = mid + 1;
            } else
                high = mid - 1;
        }
        return ans;
    }
    private boolean ok(int k, int n) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (arr[i][j] == 1) {
                    int rightSum = 0, leftSum = 0, upSum = 0, downSum = 0;

                    rightSum += rowPref[i][Math.min(j + k - 1, n - 1)];
                    if (j - 1 >= 0)
                        rightSum -= rowPref[i][j - 1];

                    leftSum += rowPref[i][j];
                    if (j - k >= 0)
                        leftSum -= rowPref[i][j - k];

                    upSum += colPref[j][i];
                    if (i - k >= 0)
                        upSum -= colPref[j][i - k];

                    downSum += colPref[j][Math.min(i + k - 1, n - 1)];
                    if (i - 1 >= 0)
                        downSum -= colPref[j][i - 1];
                    if (rightSum >= k && leftSum >= k && upSum >= k && downSum >= k)
                        return true;
                }
            }
        }
        return false;
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here