417. Pacific Atlantic Water Flow¶

Difficulty: Medium

417. Pacific Atlantic Water Flow

Medium

There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.

The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).

The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.

Return a 2D list of grid coordinates result where result[i] = [r_i, c_i] denotes that rain water can flow from cell (r_i, c_i) to both the Pacific and Atlantic oceans.

Example 1:

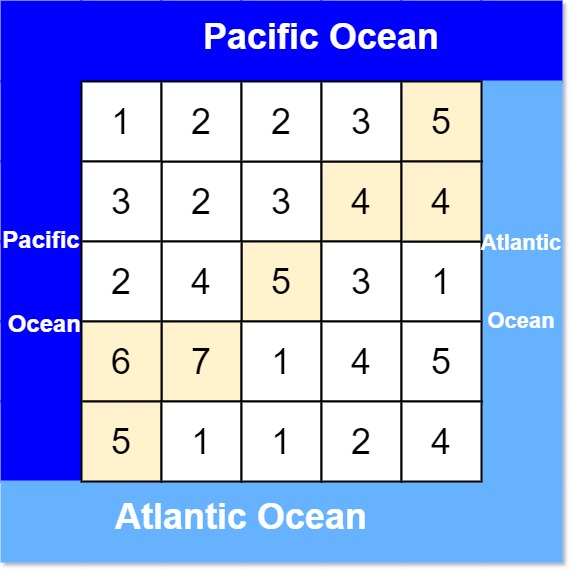
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0,4]: [0,4] -> Pacific Ocean 
       [0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean 
       [1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean 
       [1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean 
       [2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean 
       [3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean 
       [3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean 
       [4,0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.

Example 2:

Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.

Constraints:

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 10⁵

Solution¶

class Solution {
    static class Pair {
        int row, col;
        public Pair(int row, int col) {
            this.row = row;
            this.col = col;
        }
        @Override
        public String toString() {
            return "(" + row + " " + col + ")";
        }
    }
    public List<List<Integer >> pacificAtlantic(int[][] heights) {
        int n = heights.length;
        int m = heights[0].length;
        int vis1[][] = new int[n + 1][m + 1];
        int vis2[][] = new int[n + 1][m + 1];

        for (int j = 0; j < m; j++)
            if (vis1[0][j] == 0)
                bfs(0, j, heights, vis1);

        for (int i = 0; i < n; i++)
            if (vis1[i][0] == 0)
                bfs(i, 0, heights, vis1);
        for (int i = 0; i < n; i++)
            if (vis2[i][m - 1] == 0)
                bfs(i, m - 1, heights, vis2);

        for (int j = 0; j < m; j++)
            if (vis2[n - 1][j] == 0)
                bfs(n - 1, j, heights, vis2);

        List<List<Integer >> res = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (vis1[i][j] == 1 && vis2[i][j] == 1) {
                    List<Integer> temp = new ArrayList<>();
                    temp.add(i);
                    temp.add(j);
                    res.add(new ArrayList<>(temp));
                }
            }
        }
        return res;
    }

    private void bfs(int row, int col, int heights[][], int vis[][]) {
        int n = heights.length, m = heights[0].length;
        vis[row][col] = 1;
        int dir[][] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
        Queue<Pair> q = new LinkedList<>();
        q.offer(new Pair(row, col));
        while (q.size() > 0) {
            int cr = q.peek().row;
            int cc = q.peek().col;
            q.poll();
            for (int dire[] : dir) {
                int nr = cr + dire[0], nc = cc + dire[1];
                if (nr < n && nc < m && nr >= 0 && nc >= 0 && vis[nr][nc] == 0 && heights[nr][nc] >= heights[cr][cc]) {
                    q.offer(new Pair(nr, nc));
                    vis[nr][nc] = 1;
                }
            }
        }
    }
}

Complexity Analysis¶

Time Complexity: O(?)
Space Complexity: O(?)

Approach¶

Detailed explanation of the approach will be added here